
如图,直线y=2x-2与x轴交于点A,抛物线y=ax2+bx+c的对称轴是直线x=3,抛物线经过点A,且顶点P在直线y=2x-2上.

(1)求A、P两点的坐标及抛物线y=ax2+bx+c的解析式;
(2)画出抛物线的草图,并观察图象写出不等式ax2+bx+c>0的解集.
(1)A(1,0),P(3,4),y=-x2+6x-5;(2)1<x<5
【解析】
试题分析:(1)把y=0、x=3分别代入y=2x-2,即可求得A、P两点的坐标,由点P为抛物线的顶点坐标,则可设出顶点式,再将A点的坐标代入,即可求得抛物线的解析式,最后化为一般式即可;
(2)先画出抛物线的草图,再求出抛物线与x轴的交点坐标,最后根据图象的特征即可求得结果.
(1)对于y=2x-2,
当y=0时,x=1.
当x=3时,y=4.
∴ A(1,0),P(3,4).
设抛物线的解析式为y=a(x-3)2+4.
将A点的坐标代入,得a(1-3)2+4=0,解得a=-1
∴ 抛物线的解析式为 y=-(x-3)2+4,
即 y=-x2+6x-5.
(2)抛物线的草图如图所示:

解方程-x2+6x-5=0,得x1=1,x2=5.
∴ 不等式-x2+6x-5>0的解集是1<x<5.
考点:二次函数的图象
点评:在求二次函数的解析式的问题时,若知道图象的顶点坐标或对称轴,解析式一般设成顶点式.


科目:初中数学 来源:学习周报 数学 沪科八年级版 2009-2010学年 第6期 总162期 沪科版 题型:044
如图,直线y=2x+4与y=-x+4相交于点(0,4),结合图象求:

(1)方程组![]() 的解;
的解;
(2)不等式2x+4>4-x的解集;
(3)不等式组![]() 的解集;
的解集;
(4)任意写出一个与直线y=-x+4、y=2x+4相交于同一点的直线方程.
查看答案和解析>>
科目:初中数学 来源:学习周报 数学 北师大八年级版 2009-2010学年 第19-26期 总第175-182期 北师大版 题型:013
如图,直线
y=2x-4和直线y=-3x+1交于一点,则方程组
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源:四川省乐山市2012年高中阶段教育学校招生统一考试数学试卷 题型:044
如图,直线y=2x+2与y轴交于A点,与反比例函数y=![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
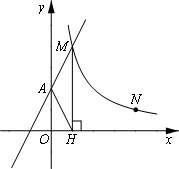
(1)求k的值;
(2)点N(a,1)是反比例函数y=![]() (x>0)图像上的点,在x轴上是否存在点P,使得PM+PN最小,若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图像上的点,在x轴上是否存在点P,使得PM+PN最小,若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2013届山东省济宁地区九年级第一学期期末考试数学试卷(带解析) 题型:解答题
如图,直线y=2x-2与x轴交于点A,抛物线y=ax2+bx+c的对称轴是直线x=3,抛物线经过点A,且顶点P在直线y=2x-2上.
(1)求A、P两点的坐标及抛物线y=ax2+bx+c的解析式;
(2)画出抛物线的草图,并观察图象写出不等式ax2+bx+c>0的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com