
【题目】(1)如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=![]() ∠BAD.求证:EF=BE+FD;
∠BAD.求证:EF=BE+FD;

(2)如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=![]() ∠BAD,(1)中的结论是否仍然成立?
∠BAD,(1)中的结论是否仍然成立?

(3)如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=![]() ∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.

【答案】(1)证明见解析;(2)(2)(1)中的结论EF=BE+FD仍然成立;(3)结论EF=BE+FD不成立,应当是EF=BE﹣FD,证明见解析.
【解析】试题分析:(1)可通过构建全等三角形来实现线段间的转换.延长EB到G,使BG=DF,连接AG.目的就是要证明三角形AGE和三角形AEF全等将EF转换成GE,那么这样EF=BE+DF了,于是证明两组三角形全等就是解题的关键.三角形ABE和AEF中,只有一条公共边AE,我们就要通过其他的全等三角形来实现,在三角形ABG和AFD中,已知了一组直角,BG=DF,AB=AD,因此两三角形全等,那么AG=AF,∠1=∠2,那么∠1+∠3=∠2+∠3=∠EAF=![]() ∠BAD.由此就构成了三角形ABE和AEF全等的所有条件(SAS),那么就能得出EF=GE了.
∠BAD.由此就构成了三角形ABE和AEF全等的所有条件(SAS),那么就能得出EF=GE了.
(2)思路和作辅助线的方法与(1)完全一样,只不过证明三角形ABG和ADF全等中,证明∠ABG=∠ADF时,用到的等角的补角相等,其他的都一样.因此与(1)的结果完全一样.
(3)按照(1)的思路,我们应该通过全等三角形来实现相等线段的转换.就应该在BE上截取BG,使BG=DF,连接AG.根据(1)的证法,我们可得出DF=BG,GE=EF,那么EF=GE=BE-BG=BE-DF.所以(1)的结论在(3)的条件下是不成立的.
(1)延长EB到G,使BG=DF,连接AG.
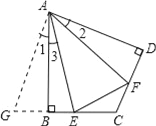
∵∠ABG=∠ABC=∠D=90°,AB=AD,
∴△ABG≌△ADF.
∴AG=AF,∠1=∠2.
∴∠1+∠3=∠2+∠3=∠EAF=![]() ∠BAD.
∠BAD.
∴∠GAE=∠EAF.
又AE=AE,
∴△AEG≌△AEF.
∴EG=EF.
∵EG=BE+BG.
∴EF=BE+FD
(2)(1)中的结论EF=BE+FD仍然成立.
(3)结论EF=BE+FD不成立,应当是EF=BE﹣FD.
证明:在BE上截取BG,使BG=DF,连接AG.
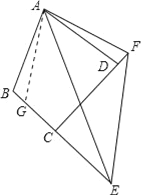
∵∠B+∠ADC=180°,∠ADF+∠ADC=180°,
∴∠B=∠ADF.
∵AB=AD,
∴△ABG≌△ADF.
∴∠BAG=∠DAF,AG=AF.
∴∠BAG+∠EAD=∠DAF+∠EAD
=∠EAF=![]() ∠BAD.
∠BAD.
∴∠GAE=∠EAF.
∵AE=AE,
∴△AEG≌△AEF.
∴EG=EF
∵EG=BE﹣BG
∴EF=BE﹣FD.


科目:初中数学 来源: 题型:
【题目】如图,△AOB中,∠O=90°,AO=8cm,BO=6cm,点C从A点出发,在边AO上以2cm/s的速度向O点运动,与此同时,点D从点B出发,在边BO上以1.5cm/s的速度向O点运动,过OC的中点E作CD的垂线EF,则当点C运动了__s时,以C点为圆心,1.5cm为半径的圆与直线EF相切.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列等式由左边到右边的变形中,属于因式分解的是( )
A.(a﹣2)(a+2)=a2﹣4
B.8x2y=8×x2y
C.m2﹣1+n2=(m+1)(m﹣1)+n2
D.x2+2x﹣3=(x﹣1)(x+3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象的对称轴是直线
的图象的对称轴是直线![]() ,则下列理论:①
,则下列理论:①![]() ,
, ![]() ②
②![]() ,③
,③![]() ,④
,④![]() ,⑤当
,⑤当![]() 时,
时, ![]() 随
随![]() 的增大而减小,其中正确的是( ).
的增大而减小,其中正确的是( ).

A. ①②③ B. ②③④ C. ③④⑤ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由四个小正方形拼接成的L形图案,按下列 要求画出图形。

(1)请你用两种方法分别在L形图案中添画一个小正方形,使它成为轴对称图形;
(2)请你在L形图案中添画一个小正方形,使它成为中心对称图形。
(3)请你在L}形图案中移动一个小正方形,使它成为既是中心对称图形,又是轴对称图形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知三条不同的直线a、b、c在同一平面内,下列四条命题:
①如果a∥b,a⊥c,那么b⊥c; ②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.
其中真命题的是 . (填写所有真命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com