
 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
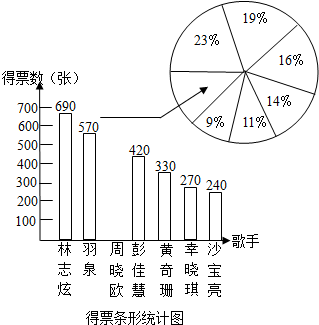 今年初湖南台“我是歌手”栏目受到广泛关注,某期比赛结果统计如下,并制作成统计图,请根据下列统计情况,回答下列问题.
今年初湖南台“我是歌手”栏目受到广泛关注,某期比赛结果统计如下,并制作成统计图,请根据下列统计情况,回答下列问题.| 歌手 | 得票数(张) | 得票率 |
| 林志炫 | 690 | 23% |
| 羽泉 | 570 | 19% |
| 周晓欧 | 480 | 16% |
| 彭佳慧 | 420 | 14% |
| 黄奇珊 | 330 | 11% |
| 幸晓琪 | 270 | 9% |
| 沙宝亮 | 240 | |
| 合计 | 3000 | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
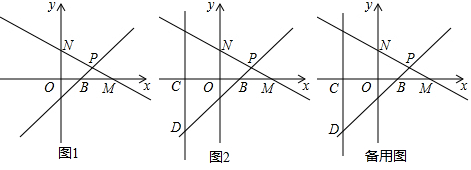
 如图,A、B两地之间有一座山,火车原来从A地到B地经过C地沿折线A→C→B行驶,现开通隧道后,火车沿直线AB行驶.已知AC=200千米,∠A=30°,∠B=45°,则隧道开通后,火车从A地到B地比原来少走多少千米(结果保留整数,$\sqrt{2}≈1.414,\sqrt{3}$≈1.732)?
如图,A、B两地之间有一座山,火车原来从A地到B地经过C地沿折线A→C→B行驶,现开通隧道后,火车沿直线AB行驶.已知AC=200千米,∠A=30°,∠B=45°,则隧道开通后,火车从A地到B地比原来少走多少千米(结果保留整数,$\sqrt{2}≈1.414,\sqrt{3}$≈1.732)?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
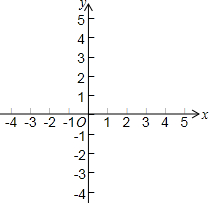 利用函数图象解方程组$\left\{\begin{array}{l}{3x+2y=5}\\{2x-y=1}\end{array}\right.$.
利用函数图象解方程组$\left\{\begin{array}{l}{3x+2y=5}\\{2x-y=1}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com