
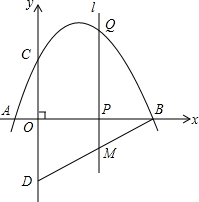
 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{5}{2}$x+3 与 x 轴交于点 A,点 B,与 y 轴交于点C,点D 与点C关于 x 轴对称,点 P 是 x 轴上的一个动点,设点P 的坐标为(m,0),过点 P 作 x 轴的垂线 l 交抛物线于点 Q.
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{5}{2}$x+3 与 x 轴交于点 A,点 B,与 y 轴交于点C,点D 与点C关于 x 轴对称,点 P 是 x 轴上的一个动点,设点P 的坐标为(m,0),过点 P 作 x 轴的垂线 l 交抛物线于点 Q.分析 (1)先求得点A、B、C的坐标,然后依据轴对称图形的性质可求得点D的坐标,然后依据待定系数法可求得BD的解析式;
(2)设点P 的坐标为(m,0),则点Q(m,$-\frac{1}{2}$m2+$\frac{5}{2}$m+3),M(m,$\frac{1}{2}$m-3),依据△QBD的面积=$\frac{1}{2}$AB•QP列出△QBD的面积与m的函数关系式,利用配方法可求得m的值,从而得到点Q的坐标,过点E作EF⊥BD,垂足为F.先证明EF=$\frac{\sqrt{5}}{5}$BE,则QE+$\frac{\sqrt{5}}{5}$EB=QE+EF.当点Q、E、F在一条直线上时,QE+$\frac{\sqrt{5}}{5}$EB有最小值;
(3)当∠QDB=90°时或当∠QBD=90°时,求得求得DQ或BD的解析式,然后求得直线与抛物线的交点坐标即可,当∠BQD=90°时.设点Q的坐标为(x,$-\frac{1}{2}$x2+$\frac{5}{2}$x+3),则QD2=x2+($-\frac{1}{2}$x2+$\frac{5}{2}$x+6)2,BQ2=(x-6)2+(-$\frac{1}{2}$x2+$\frac{5}{2}$x+3)2,BD2=45,然后依据勾股定理列方程求解即可.
解答 解:(1)当y=0时,$-\frac{1}{2}$x2+$\frac{5}{2}$x+3=0,解得x1=6,x2=-1,
∴A(-1,0)、B(6,0),
当x=0时,y=3,则C(0,3).
∵点 D 与点 C 关于 x 轴对称,
∴点D为(0,-3).
设直线BD的解析式为y=kx+b,将D(0,-3)和B (6,0)分别代入得$\left\{\begin{array}{l}{b=-3}\\{6k+b=0}\end{array}\right.$,
解得:k=$\frac{1}{2}$,b=-3.
∴直线BD的解析式为y=$\frac{1}{2}$x-3.
(2)设点P 的坐标为(m,0),则点Q(m,$-\frac{1}{2}$m2+$\frac{5}{2}$m+3),M(m,$\frac{1}{2}$m-3).
△QBD的面积=$\frac{1}{2}$AB•QP=$\frac{1}{2}$×6×($-\frac{1}{2}$m2+$\frac{5}{2}$m+3-$\frac{1}{2}$m+3)=-$\frac{3}{2}$(m-2)2+24,
∴当m=2时,△QBD的面积有最大值,此时Q(2,6).
如图1所示:过点E作EF⊥BD,垂足为F.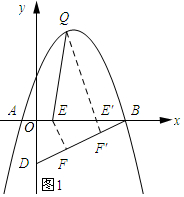
在Rt△OBD中,OB=6,OD=3,则BD=3$\sqrt{5}$,
∴tan∠EBF=tan∠OBD=$\frac{OD}{BD}$=$\frac{\sqrt{5}}{5}$.
∴EF=$\frac{\sqrt{5}}{5}$BE.
∴QE+$\frac{\sqrt{5}}{5}$EB=QE+EF.
∴当点Q、E、F在一条直线上时,QE+$\frac{\sqrt{5}}{5}$EB有最小值.
过点Q作QF′⊥BC,垂足为F′,QF′交OB与点E′.
设QF′的解析式为y=-2x+b,将点Q的坐标代入得:-4+b=6,解得b=10,
∴QF′的解析式为y=-2x+10.
当y=0时,-2x+10=0,解得x=5,
∴点E′的坐标为(5,0).即点E的坐标为(5,0)时QE+$\frac{\sqrt{5}}{5}$EB有最小值.
∴QE+$\frac{\sqrt{5}}{5}$EB的最小值=$\sqrt{(5-2)^{2}+(6-0)^{2}}$=3$\sqrt{5}$+$\frac{\sqrt{5}}{5}$=$\frac{16\sqrt{5}}{5}$.
(3)当∠QDB=90°时,DQ的解析式为y=-2x-3.
将y=-2x-3与y=$-\frac{1}{2}$x2+$\frac{5}{2}$x+3联立解得:x=$\frac{9+\sqrt{129}}{2}$或x=$\frac{9-\sqrt{129}}{2}$.
∴点Q的坐标为($\frac{9+\sqrt{129}}{2}$,-12-$\sqrt{129}$)或($\frac{9-\sqrt{129}}{2}$,-12+$\sqrt{129}$)
当∠QBD=90°时,DB的解析式为y=-2x+12,
将y=-2x+12与y=$-\frac{1}{2}$x2+$\frac{5}{2}$x+3联立解得x=3或x=6(舍去).
∴点Q的坐标为(3,6).
当∠BQD=90°时.设点Q的坐标为(x,$-\frac{1}{2}$x2+$\frac{5}{2}$x+3),则QD2=x2+($-\frac{1}{2}$x2+$\frac{5}{2}$x+6)2,BQ2=(x-6)2+(-$\frac{1}{2}$x2+$\frac{5}{2}$x+3)2,BD2=45,
依据勾股定理可知:x2+($-\frac{1}{2}$x2+$\frac{5}{2}$x+6)2+(x-6)2+(-$\frac{1}{2}$x2+$\frac{5}{2}$x+3)2=45,解得:x=6$\frac{1}{3}$或x=6(舍去).
将x=6$\frac{1}{3}$代入抛物线的解析式得:y=-$\frac{11}{9}$.
∴点Q的坐标为(6$\frac{1}{3}$,-$\frac{11}{9}$).
综上所述,点Q的坐标为($\frac{9+\sqrt{129}}{2}$,-12-$\sqrt{129}$)或($\frac{9-\sqrt{129}}{2}$,-12+$\sqrt{129}$)或(3,6)或(6$\frac{1}{3}$,-$\frac{11}{9}$).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数的解析式,勾股定理、锐角三角函数的定义、二次函数的性质,明确当点Q、E、F在一条直线上时,QE+$\frac{\sqrt{5}}{5}$EB的长度由最小值是解题的关键,依据勾股定理列出关于x的方程是解答问题(3)的关键.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:选择题

| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在四边形OABC中,AB∥OC,∠OAB=90°,∠OCB=60°,AB=2,OA=2$\sqrt{3}$.
在四边形OABC中,AB∥OC,∠OAB=90°,∠OCB=60°,AB=2,OA=2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
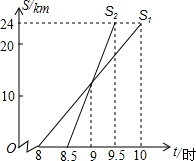 小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家,妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程S(km)与北京时间t(时)的函数图象如图所示.根据图象得到小亮结论,其中错误的是( )
小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家,妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程S(km)与北京时间t(时)的函数图象如图所示.根据图象得到小亮结论,其中错误的是( )| A. | 小亮骑自行车的平均速度是12km/h | |
| B. | 妈妈比小亮提前0.5小时到达姥姥家 | |
| C. | 9:00妈妈追上小亮 | |
| D. | 妈妈在距家13km处追上小亮 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com