
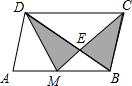
 如图所示,已知M是平行四边形ABCD的AB边的中点,CM交BD于点E,BD=3BE,则图中阴影部分面积与平行四边形ABCD面积之比为
如图所示,已知M是平行四边形ABCD的AB边的中点,CM交BD于点E,BD=3BE,则图中阴影部分面积与平行四边形ABCD面积之比为科目:初中数学 来源: 题型:
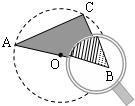 14、已知,AB是⊙O的直径,且C是圆上一点,小聪透过平举的放大镜从正上方看到水平桌面上的三角形图案的∠B(如图所示),那么下列关于∠A与放大镜中的∠B关系描述正确的是( )
14、已知,AB是⊙O的直径,且C是圆上一点,小聪透过平举的放大镜从正上方看到水平桌面上的三角形图案的∠B(如图所示),那么下列关于∠A与放大镜中的∠B关系描述正确的是( )查看答案和解析>>
科目:初中数学 来源: 题型:
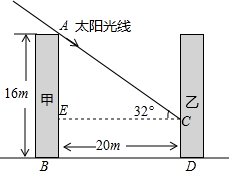 某房地产集团筹建一小区,居民楼均为平顶条式,南北朝向,楼高统一为16m(五层).已知该城市冬至正午时分太阳高度最低,太阳光线与水平线的夹角为32°,如果南北两楼相隔仅有20m(如图所示),试求:
某房地产集团筹建一小区,居民楼均为平顶条式,南北朝向,楼高统一为16m(五层).已知该城市冬至正午时分太阳高度最低,太阳光线与水平线的夹角为32°,如果南北两楼相隔仅有20m(如图所示),试求:查看答案和解析>>
科目:初中数学 来源: 题型:
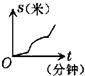
 小明同学骑自行车在上学的路上要经过两座山梁,行走的路线如图所示.已知上山的速度为v1米/分钟,平路的速度为v2米/分钟,下山的速度为v3米/分钟,其中v1<v2<v3.那么,小明同学上学骑自行车行走的路程S(米)与所用的时间t(分钟)的函数关系,可能是下面图象中的( )
小明同学骑自行车在上学的路上要经过两座山梁,行走的路线如图所示.已知上山的速度为v1米/分钟,平路的速度为v2米/分钟,下山的速度为v3米/分钟,其中v1<v2<v3.那么,小明同学上学骑自行车行走的路程S(米)与所用的时间t(分钟)的函数关系,可能是下面图象中的( )查看答案和解析>>
科目:初中数学 来源: 题型:单选题
 小明同学骑自行车在上学的路上要经过两座山梁,行走的路线如图所示.已知上山的速度为v1米/分钟,平路的速度为v2米/分钟,下山的速度为v3米/分钟,其中v1<v2<v3.那么,小明同学上学骑自行车行走的路程S(米)与所用的时间t(分钟)的函数关系,可能是下面图象中的
小明同学骑自行车在上学的路上要经过两座山梁,行走的路线如图所示.已知上山的速度为v1米/分钟,平路的速度为v2米/分钟,下山的速度为v3米/分钟,其中v1<v2<v3.那么,小明同学上学骑自行车行走的路程S(米)与所用的时间t(分钟)的函数关系,可能是下面图象中的
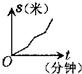
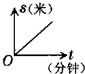
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com