练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．如图，AB是⊙O的直径，点C是圆上一点，∠BAC=70°，则∠OCB等于（　　）
    A．70°B．20°C．140°D．35°

    分析 先根据圆周角定理求出∠ACB的度数，再由直角三角形的性质求出∠B的度数，根据等腰三角形的性质即可得出结论．

    解答 解：∵AB是⊙O的直径，
    ∴∠ACB=90°．
    ∵∠BAC=70°，
    ∴∠B=90°-70°=20°．
    ∵OB=OC，
    ∴∠OCB=∠B=20°．
    故选B．

    点评 本题考查的是圆周角定理，熟知直径所对的圆周角是直角是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    11．如图，两个反比例函数y=$\frac{1}{x}$和y=$\frac{-2}{x}$的图象分别是C1和C2，点P是C1上自左向右运动的动点，PD⊥x轴，垂足为C，交C2于点D，PA⊥y轴，垂足为B，交C2于点A，则关于四边形ABCD的面积说法正确的是（　　）
    A．逐渐变大B．逐渐变小C．不变，面积为$\frac{9}{2}$D．不变，面积为4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．已知：如图，在菱形ABCD中，∠BAD=44°，AB的垂直平分线交对角线AC于点F，垂足为E，连接DF，则∠CDF等于（　　）
    A．112°B．114°C．116°D．118°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，已知抛物线m：y=ax2-6ax+c（a＞0）的顶点A在x轴上，并过点B（0，1），直线n：y=-$\frac{1}{2}$x+$\frac{7}{2}$与x轴交于点D，与抛物线m的对称轴l交于点F，过B点的直线BE与直线n相交于点E（-7，7）．
    （1）求抛物线m的解析式；
    （2）P是l上的一个动点，若以B，E，P为顶点的三角形的周长最小，求点P的坐标；
    （3）抛物线m上是否存在一动点Q，使以线段FQ为直径的圆恰好经过点D？若存在，求点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．用一枚直径为25mm的硬币完全覆盖一个正六边形，则这个正六边形的最大边长是（　　）
    A．$\frac{25}{2}$mmB．$\frac{25}{2}$$\sqrt{3}$mmC．$\frac{25}{4}$mmD．$\frac{25}{4}$$\sqrt{3}$mm

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．已知直线y=x-3与函数y=$\frac{2}{x}$的图象相交于点（a，b），则代数式a2+b2的值是（　　）
    A．13B．11C．7D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

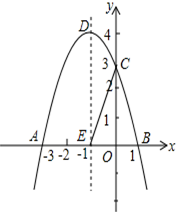    13．如图，关于y=-x2+bx+c的二次函数y=-x2+bx+c经过点A（-3，0），点C（0，3），点D为二次函数的顶点，DE为二次函数的对称轴，点E在x轴上．
    （1）求抛物线的解析式及顶点D的坐标；
    （2）在图中求一点G，使以G、A、E、C为顶点的四边形是平行四边形，请直接写出点G的坐标；
    （3）在抛物线A、C两点之间有一点F，使△FAC的面积最大，求该点坐标；
    （4）直线DE上是否存在点P到直线AD的距离与到轴的距离相等？若存在，请求出点P，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．不等式x+7＜3x+1的解集是（　　）
    A．x＜-3B．x＞3C．x＜-4D．x＞4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

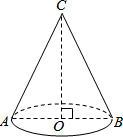    11．如图，一个圆锥形漏斗的底面半径OB=6cm，高OC=8cm．则这个圆锥漏斗的侧面积是（　　）
    A．30cm2B．30πcm2C．60πcm2D．120cm2

    查看答案和解析>>

    同步练习册答案