练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，将斜边长为4的直角三角板放在直角坐标系xOy中，两条直角边分别与坐标轴重合，P为斜边的中点．现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是（　　）

    A. （，1） B. （1，﹣） C. （2，﹣2） D. （2，﹣2）

    B 【解析】试题分析：根据题意画出△AOB绕着O点顺时针旋转120°得到的△COD，连接OP，OQ，过Q作QM⊥y轴，由旋转的性质得到∠POQ=120°，根据AP=BP=OP=2，得到∠AOP度数，进而求出∠MOQ度数为30°，在直角三角形OMQ中求出MQ=1，OM=，即可确定出Q的坐标为（1，﹣），故选B．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年九年级数学人教版上册：第24章 圆 单元测试卷 题型：解答题

    如图，⊙O是△ABC的外接圆，AB是⊙O的直径，AB=8．

    （1）利用尺规，作∠CAB的平分线，交⊙O于点D；（保留作图痕迹，不写作法）

    （2）在（1）的条件下，连接CD，OD，若AC=CD，求∠B的度数；

    （3）在（2）的条件下，OD交BC于点E．求出由线段ED，BE，所围成区域的面积．（其中表示劣弧，结果保留π和根号）

    （1）作图见解析；（2）30°；（3）． 【解析】 试题分析：（1）作AP平分∠CAB交⊙O于D； （2）由等腰三角形性质得到∠CAD=∠ADC．又由∠ADC=∠B，得到∠CAD=∠B． 再根据角平分线定义得到∠CAD=∠DAB=∠B．由于直径所对圆周角为90°，得到∠ACB=90°，从而得到∠B的度数； （3）先得到△OEB是30°角的直角三角形，从而得出OE，EB...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学人教版上册：第3章 一元一次方程 单元测试卷 题型：单选题

    方程2x＋3＝7的解是( )

    A. x＝5 B. x＝4 C. x＝3.5 D. x＝2

    D 【解析】试题分析：2x+3=7，移项合并得2x=4，解得x=2，故答案选D.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学人教版上册：第23章 旋转 单元测试卷 题型：填空题

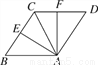
    如图，将等边△ABC绕顶点A按顺时针方向旋转，使边AB与AC重合得△ACD，BC的中点E的对应点为F，则∠EAF的度数为_______.

    60° 【解析】∵将等边△ABC绕顶点A顺时针方向旋转，使边AB与AC重合得△ACD，BC的中点E的对应点为F， ∴旋转角为60°，E，F是对应点， 则∠EAF的度数为：60°．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学人教版上册：第23章 旋转 单元测试卷 题型：单选题

    下列图案中，是轴对称图形但不是中心对称图形的是（ ）

    A. B. C. D.

    A 【解析】A是轴对称图形，不是中心对称图形，故正确； B是轴对称图形也是中心对称图形，故不正确； C既不是轴对称图形也不是中心对称图形，故不正确； D不是轴对称图形，是中心对称图形，故不正确； 故选A.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学人教版上册：第25章 概率初步 单元测试卷 题型：解答题

    如图，一条直线上有两只蚂蚁，甲蚂蚁在点A处，乙蚂蚁在点B处，假设两只蚂蚁同时出发，爬行方向只能沿直线AB在“向左”或“向右”中随机选择，并且甲蚂蚁爬行的速度比乙蚂蚁快．

    (1)甲蚂蚁选择“向左”爬行的概率为；

    (2)利用列表或画树状图的方法求两只蚂蚁开始爬行后会“触碰到”的概率．

    （1）；（2）. 【解析】试题分析：（1）根据概率的求法，找准两点：①全部等可能情况的总数；②符合条件的情况数目；二者的比值就是其发生的概率．因此，由爬行方向只能沿直线AB在“向左”或“向右”中随机选择，直接利用概率公式求解即可求得答案． （2）根据题意画出树状图或列表，然后由图表求得所有等可能的结果与两只蚂蚁开始爬行后会“触碰到”的情况，再利用概率公式即可求得答案． 试题解析：...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学人教版上册：第25章 概率初步 单元测试卷 题型：填空题

    在一个不透明的箱子中装有4件同型号的产品，其中合格品3件、不合格品1件，现在从这4件产品中随机抽取2件检测，则抽到的都是合格品的概率是　　．

    【解析】试题分析：画树状图得： ∵共有12种等可能的结果，抽到的都是合格品的有6种情况，∴抽到的都是合格品的概率是：=． 故答案为：．

    查看答案和解析>>

    科目：初中数学 来源：安徽省蚌埠市2017届九年级下学期中考二模数学试卷 题型：解答题

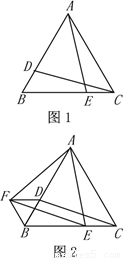
    如图1，图2，△ABC是等边三角形，D、E分别是AB、BC边上的两个动点（与点A、B、C不重合），始终保持BD=CE.

    （1）当点D、E运动到如图1所示的位置时,求证：CD=AE.

    （2）把图1中的△ACE绕着A点顺时针旋转60°到△ABF的位置（如图2），分别连结DF、EF.

    ①找出图中所有的等边三角形(△ABC除外)，并对其中一个给予证明；

    ②试判断四边形CDFE的形状,并说明理由.

    （1）证明见解析；（2）①图中有2个正三角形，分别是△BDF，△AFE，证明见解析；②四边形CDFE是平行四边形，理由见解析. 【解析】（1）∵△ABC是正三角形， ∴BC=CA，∠B=∠ECA=60°. …………………………（2分） 又∵BD=CE， ∴△BCD≌△CAE. …………………………（3分） ∴CD=AE. …………………………（4分） （2）① ...

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：第二十七章 达标检测卷 题型：单选题

    如图，在△ABC中，DE∥BC， ，DE=4，则BC的长是（　　）

    A. 8 B. 10 C. 11 D. 12

    D 【解析】试题解析：∵， ∴， ∵在△ABC中，DE∥BC， ∴， ∵DE=4， ∴BC=3DE=12． 故选D．

    查看答案和解析>>

    同步练习册答案