
【题目】甲乙两人轮流在黑板上写下不超过 ![]() 的正整数(每次只能写一个数),规定禁止在黑板上写已经写过的数的约数,最后不能写的为失败者,如果甲写第一个,那么,甲写数字( )时有必胜的策略.
的正整数(每次只能写一个数),规定禁止在黑板上写已经写过的数的约数,最后不能写的为失败者,如果甲写第一个,那么,甲写数字( )时有必胜的策略.
A. 10 B. 9 C. 8D.6
【答案】D
【解析】
解答此题的关键是第一个数字写出后,后面可写的数字是偶数个,并且可以分成不是约数关系的几组.
对于选项A:当甲写10时,乙可以写3、4、6、7、8、9,如果乙写7,则乙必胜,因为无论甲写3,4,6,8,9这五个数中的6(连带3)或8(连带4),乙可以写4或3,剩下2个数字;当甲写3或4时,乙可以写8(连带4)或6(连带3),剩下偶数个数字甲最后不能写,乙必胜;
对于选项B:当甲写9后,乙可以写2、4、5、6、7、8、10,如果乙写6,则乙必胜,因为剩下4、5、7、8、10这5个数中,无论甲写8(连带4)或10(连带5),乙可以写5或4;当甲写4或5时,乙可以写10(连带5)或8(连带4),甲最后不能写,乙必胜;
对于选项C:当甲写8时,乙可以写3、5、6、7、9、10,当乙写6(或10)时,甲就必须写10(或6),因为乙写6(或10)后,连带3(或5)也不能写了,这样才能保证剩下能写的数有偶数个,甲才可以获胜;
对于选项D: 甲先写6,由于6的约数有1,2,3,6,接下来乙可以写的数只有4、5、7、8、9、10,把这6个数分成三组:(4,7)、(5,8)、(9,10),当然也可(4,5)、(8,10)、(7,9)或(4,9)、(5,7)、(8,10)等等,只要组内两数大数不是小数的倍数即可,这样,乙写某组数中的某个数时,甲就写同组中的另一数,从而甲一定写最后一个,甲必获胜,
综上可知,只有甲先写6,才能必胜,
故选:D.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】(本题满分9分)如图,以⊿ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E,且![]() .
.
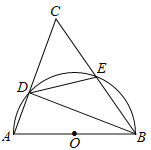
(1)试判断⊿ABC的形状,并说明理由;
(2)已知半圆的半径为5,BC=12,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
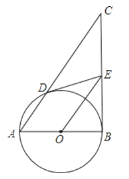
【题目】已知:以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,过点D作⊙O的切线交BC边于点E.
(1)如图,求证:EB=EC=ED;
(2)试问在线段DC上是否存在点F,满足BC2=4DFDC?若存在,作出点F,并予以证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(–1,2),与x轴的一个交点A在点(–3,0)和(–2,0)之间,其部分图象如下图,则以下结论:①b2–4ac<0;②a+b+c<0;③c–a=2;④方程ax2+bx+c–2=0有两个相等的实数根.其中正确结论的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(﹣![]() ,
,![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同.
(1)求摸出1个球是白球的概率;
(2)摸出1个球,记下颜色后放回,并搅均,再摸出1个球.求两次摸出的球恰好颜色不同的概率(要求画树状图或列表);
(3)现再将n个白球放入布袋,搅均后,使摸出1个球是白球的概率为![]() .求n的值.
.求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,E为AB的中点.

(1)求证:△ADC∽△ACB;
(2)CE与AD有怎样的位置关系?试说明理由;
(3)若AD=4,AB=6,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线,与边BC交于点E,若AD=![]() , AC=3.则DE长为( )
, AC=3.则DE长为( )
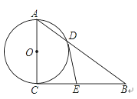
A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
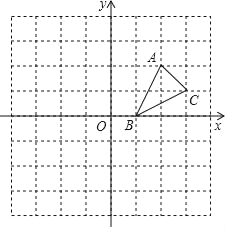
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2,并写出点C2的坐标;
(3)△A1B1C1与△A2B2C2成中心对称吗?若成中心对称,写出对称中心的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com