
 如图,抛物线经过点A(-1,0)和B(0,2$\sqrt{2}$),对称轴为x=$\frac{5}{4}$.
如图,抛物线经过点A(-1,0)和B(0,2$\sqrt{2}$),对称轴为x=$\frac{5}{4}$.分析 (1)设抛物线的解析式为y=a(x-$\frac{5}{4}$)2+k,(a≠),把点A(-1,0)和B(0,2$\sqrt{2}$)代入,解方程组即可解决问题.
(2)首先求出A、C坐标,由∠DBP=∠DBQ,可得$\frac{PB}{BC}$=$\frac{PD}{CD}$(角平分线的性质定理,可以用面积法证明),即$\frac{\sqrt{8+(t-1)^{2}}}{\frac{9}{2}}$=$\frac{3-t}{\frac{3}{2}}$,解方程即可解决问题.
(3)存在.理由如下:首先证明∠BPC=∠BAM,分两种情形讨论①当$\frac{AM}{PB}$=$\frac{AB}{PC}$,△MAB∽△BPC,列出方程解方程即可.②当$\frac{AM}{PC}$=$\frac{AB}{PB}$时,△MAB∽CPB,列出方程解方程即可.
解答 解:(1)设抛物线的解析式为y=a(x-$\frac{5}{4}$)2+k,(a≠),
把点A(-1,0)和B(0,2$\sqrt{2}$)代入得到$\left\{\begin{array}{l}{\frac{81}{16}a+k=0}\\{\frac{25}{16}a+k=2\sqrt{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{4\sqrt{2}}{7}}\\{k=\frac{81}{28}\sqrt{2}}\end{array}\right.$,
∴y=-$\frac{4\sqrt{2}}{7}$(x-$\frac{5}{4}$)2+$\frac{81\sqrt{2}}{28}$,
∴y=-$\frac{4\sqrt{2}}{7}$x2+$\frac{10\sqrt{2}}{7}$x+2$\sqrt{2}$.
(2)令y=0得到-$\frac{4\sqrt{2}}{7}$x2+$\frac{10\sqrt{2}}{7}$x+2$\sqrt{2}$=0,解得x=$\frac{7}{2}$或-1,
∴C($\frac{7}{2}$,0),A(-1,0),AB=$\sqrt{{1}^{2}+(2\sqrt{2})^{2}}$=3,
∵AD=AB,
∴AD=3,
∴D(2,0),
∵PQ被直线BD垂直平分,
∴BP=BQ,
∴∠DBP=∠DBQ,
∴$\frac{PB}{BC}$=$\frac{PD}{CD}$(角平分线的性质定理,可以用面积法证明),
∴$\frac{\sqrt{8+(t-1)^{2}}}{\frac{9}{2}}$=$\frac{3-t}{\frac{3}{2}}$,
∴t=2或$\frac{9}{2}$,
∵t<3,
∴t=2,
∴BP=3,BQ=3,
∴VQ=$\frac{3}{2}$.
(3)存在.理由如下:
由题意P(1,0),PB=3,PC=$\frac{5}{2}$,
∵BA=BP=3,
∴∠BAP=∠BPA,
∴∠BPC=∠BAM,
①当$\frac{AM}{PB}$=$\frac{AB}{PC}$,△MAB∽△BPC,
∴$\frac{AM}{3}$=$\frac{3}{\frac{5}{2}}$,
∴AM=$\frac{18}{5}$,OM=OA+AM=$\frac{23}{5}$
∴M(-$\frac{23}{5}$,0).
②当$\frac{AM}{PC}$=$\frac{AB}{PB}$时,△MAB∽CPB,
∴$\frac{AM}{\frac{5}{2}}$=$\frac{3}{3}$,
∴AM=$\frac{5}{2}$,OM=AM+OA=$\frac{7}{2}$,
∴M(-$\frac{7}{2}$,0).
点评 本题考查二次函数综合题、线段的垂直平分线的性质、角平分线的性质定理、相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
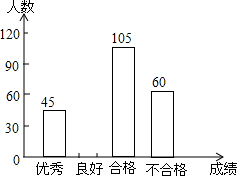 为了解今年初三学生的数学学习情况,某校对上学期的数学成绩作了统计分析,绘制得到如下图表.请结合图表所给出的信息解答下列问题:
为了解今年初三学生的数学学习情况,某校对上学期的数学成绩作了统计分析,绘制得到如下图表.请结合图表所给出的信息解答下列问题:| 成绩 | 频数 | 频率 |
| 优秀 | 45 | b |
| 良好 | a | 0.3 |
| 合格 | 105 | 0.35 |
| 不合格 | 60 | c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知∠ABC=90°,D是AB延长线上的点,AD=BC,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF,求证:FD⊥CD.
如图,已知∠ABC=90°,D是AB延长线上的点,AD=BC,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF,求证:FD⊥CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 直线l1与l2相交于点P,l1的函数表达式y=2x+3,点P的横坐标为-1,且l2交y轴于点A(0,-1).求直线l2的函数表达式及△PAB的面积.
直线l1与l2相交于点P,l1的函数表达式y=2x+3,点P的横坐标为-1,且l2交y轴于点A(0,-1).求直线l2的函数表达式及△PAB的面积.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
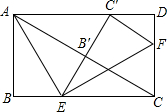 如图,在矩形ABCD中,AB=4,点E,F分别在BC,CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在直线EB′与AD的交点C′处,DF=$\frac{4}{3}$.
如图,在矩形ABCD中,AB=4,点E,F分别在BC,CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在直线EB′与AD的交点C′处,DF=$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com