
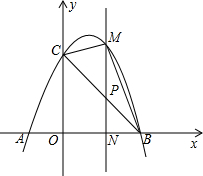
 如图,已知抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.
如图,已知抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.分析 (1)先求出C的坐标,然后令y=0,-x2+2x+3=0,求出点B的坐标,利用待定系数法求出过B,C两点的一次函数关系式;
(2)设P(x,-x+3),则M(x,-x2+2x+3),用x表示出PM,利用S△BCM=S△PMC+S△PMB,进而写出关于x的二次函数表达式,即可求出△BCM的面积最大值;
(3)过点N作CN的垂线,交对称轴于点Q,交y轴于点F,利用Rt△NFO∽Rt△CNO求出点F的坐标,求出FN的解析式,即可求出点Q的坐标.
解答 解:(1)由抛物线的解析式为y=-x2+2x+3,可得C(0,3),
令y=0,-x2+2x+3=0,解得x=3或x=-1,
∴A(-1,0),B(3,0),
设过B、C两点的一次函数解析式为y=kx+b,则有:
$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
∴直线BC的解析式为y=-x+3;
(2)设P(x,-x+3),则M(x,-x2+2x+3),
∴PM=(-x2+2x+3)-(-x+3)=-x2+3x,
∴S△BCM=S△PMC+S△PMB
=$\frac{1}{2}$PM•NO+$\frac{1}{2}$PM•NB=$\frac{1}{2}$PM(NO+BN)
=$\frac{1}{2}$PM•BO
=$\frac{3}{2}$PM,
∴S△BCM=$\frac{3}{2}$(-x2+3x)
=-$\frac{3}{2}$(x-$\frac{3}{2}$)2+$\frac{27}{8}$,
∴当x=$\frac{3}{2}$时,△BCM的面积最大,
∴N($\frac{3}{2}$,0);
(3)∵y=-x2+2x+3=-(x-1)2+4,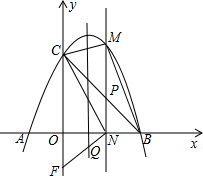
∴抛物线的对称轴为直线x=1,
过点N作CN的垂线,交对称轴于点Q,交y轴于点F,
易证Rt△NFO∽Rt△CNO,
则$\frac{OF}{ON}=\frac{ON}{OC}$,
则$\frac{OF}{\frac{3}{2}}=\frac{\frac{3}{2}}{3}$,
∴F(0,-$\frac{3}{4}$),
又∵N($\frac{3}{2}$,0),
∴直线FN的解析式为y=$\frac{1}{2}$x-$\frac{3}{4}$,
当x=1时,y=-$\frac{1}{4}$,
∴Q(1,-$\frac{1}{4}$).
点评 本题主要考查了二次函数的综合题的知识,此题涉及到待定系数法求一次函数的解析式、二次函数的性质、相似三角形的判定与性质以及三角形面积的计算,解答此题(2)问需要得到S△BCM=$\frac{3}{2}$(-x2+3x),解答(3)问需要熟练掌握三角形相似的性质,此题有一定的难度.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD的边长为4,点E是AD的中点,点F在AB上且AF=1,以EF、CF为边作平行四边形EFCG,连DG,则DG=$\sqrt{13}$.
如图,正方形ABCD的边长为4,点E是AD的中点,点F在AB上且AF=1,以EF、CF为边作平行四边形EFCG,连DG,则DG=$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x2-5x+2=0 | B. | x2-5x+1=0 | C. | 2x2+5x+2=0 | D. | 2x2-5x+1=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x-2)2-3 | B. | y=(x-2)2+3 | C. | y=(x+2)2-3 | D. | y=(x+2)2+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一个游戏的中奖概率是$\frac{1}{100}$,则做100次这样的游戏一定会中奖 | |
| B. | 为了解全国中学生的心理健康情况,应该采用普查的方式 | |
| C. | 一组数据 8,8,7,10,6,8,9 的众数和中位数都是8 | |
| D. | 若甲组数据的方差s2=0.01,乙组数据的方差s2=0.1,则乙组数据比甲组数据稳定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 甲比乙大 | B. | 乙比甲大 | C. | 甲、乙一样大 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com