
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AO����ABC�Ľ�ƽ���ߣ���OΪԲ�ģ�OCΪ�뾶����O��
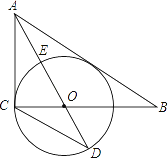
��1����֤��AB����O�����ߣ�
��2����֪AO����O�ڵ�E���ӳ�AO����O�ڵ�D��tanD=![]() ����
����![]() ��ֵ��
��ֵ��
��3���ڣ�2���������£�����O�İ뾶Ϊ3����AB�ij���
���𰸡���1��֤����������2��![]() ��3��
��3��![]()
�������������������1����O��OF��AB��F���ɽ�ƽ�����ϵĵ㵽�����ߵľ�����ȼ��ɵ�֤����2������CE��֤����ACE�ס�ADC�ɵ�![]() = tanD��
= tanD��![]() ����3�����ɹ��ɶ������AE�ij�����֤����B0F�ס�BAC����
����3�����ɹ��ɶ������AE�ij�����֤����B0F�ס�BAC����![]() ����BO="y" ��BF=z���ж�Ԫһ�η����鼴�ɽ�����⣮
����BO="y" ��BF=z���ж�Ԫһ�η����鼴�ɽ�����⣮
�����������1��֤������OF��AB��F
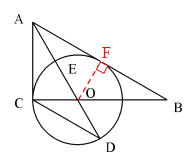
��AO����BAC�Ľ�ƽ���ߣ���ACB=90
��OC=OF
��AB����O������
��2������CE
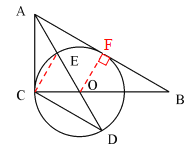
��AO����BAC�Ľ�ƽ���ߣ�
���CAE=��CAD
�ߡ�ACE���ԵĻ�����CDE���ԵĻ���ͬ��
���ACE=��CDE
���ACE�ס�ADC
��![]() = tanD��
= tanD��![]()
��3��������ACO����AE=x,
�ɹ��ɶ�����
(x��3)="(2x)" ��3 �����x="2,"
�ߡ�BFO=90��=��ACO
��֤Rt��B0F��Rt��BAC
��![]() ��
��
��BO=y BF=z
![]()
��4z=9��3y��4y=12��3z
���z=![]() y=
y=![]()
��AB=![]() ��4=
��4=![]()
���㣺Բ���ۺ��⣮
�����͡������
��������
22
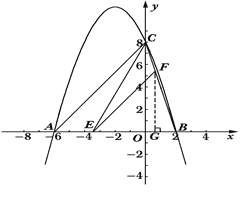
����Ŀ����֪�����κ���![]() ��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C�����е�B��x����������ϣ���C��y����������ϣ��߶�O��OC�ij���OB��OC���Ƿ���x2��10x��16��0������������A������Ϊ����6��0����
��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C�����е�B��x����������ϣ���C��y����������ϣ��߶�O��OC�ij���OB��OC���Ƿ���x2��10x��16��0������������A������Ϊ����6��0����
��1����˶��κ����ı���ʽ��
��2������E���߶�AB�ϵ�һ�����㣨���A����B���غϣ�������E��EF��AC��BC�ڵ�F������CE����AE�ij�Ϊm����CEF�����ΪS����S��m֮��ĺ�����ϵʽ����д���Ա���m��ȡֵ��Χ��
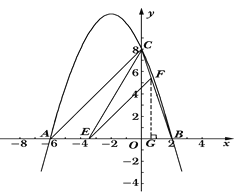
���𰸡���1��y����![]() x2��
x2��![]() x��8��2��
x��8��2��
���������������:(1)���һԪ���η��̵��������������������,��B��C�������������κ����Ľ���ʽ�Ϳɽ��
(2)����F��FG��AB������ΪG����EF��AC������BEF�ס�BAC���������Ʊ���EF������sin��FEG=sin��CAB��FG������S=S��BCE-S��BFE����S��m֮��ĺ�����ϵʽ.
��:(1���ⷽ��x2��10x��16��0��x1��2��x2��8
��B��2��0����C��0��8��
��������κ����ı���ʽΪy����![]() x2��
x2��![]() x��8
x��8
��2����AB��8��OC��8�������⣬AE��m����BE��8��m��
��OA��6��OC��8�� ��AC��10.
��EF��AC, ���BEF�ס�BAC.
��![]() ��
��![]() .������
.������![]() ��
��![]() . ��EF��
. ��EF��![]() .
.
����F��FG��AB������ΪG��
��sin��FEG��sin��CAB��![]() .��
.��![]() ��
��![]() .��
.��
��FG��![]() ��
��![]() ��8��m.
��8��m.
��S��S��BCE��S��BFE
��![]()
![]() ��0��m��8��
��0��m��8��
�㾦:���⿼����һԪ���η��̵Ľⷨ������ϵ����������ϵϵ�����������ε��ж�������,������Ǻ����Ķ��壬�����ͼ�ε�������������մ���ϵ��������κ�����ϵʽ�����������ε��ж��������ǽ����Ĺؼ�.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڴ�¥AB��ǰ����һб��CD���½ǡ�DCE=30����¥��AB=60�ף���б���µĵ�C�����¥��B������Ϊ60������б���ϵ�D�����¥��B������Ϊ45�������е�A,C,E��ͬһֱ����.
��1�����µ�C�㵽��¥����AC��ֵ��
��2�����CD�ij���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
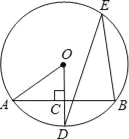
����Ŀ����ͼ��ʾ��AB����O��һ���ң�OD��AB������ΪC������O�ڵ�D����E����O�ϣ�
��1������AOD=52��������DEB�Ķ�����
��2����OC=3��OA=5����AB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
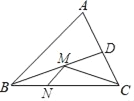
����Ŀ����ͼ�������������ABC�У�BC��6![]() ����ABC��45�㣬BDƽ�֡�ABC��M��N�ֱ���BD��BC�ϵĶ��㣬��CM+MN����Сֵ��_____��
����ABC��45�㣬BDƽ�֡�ABC��M��N�ֱ���BD��BC�ϵĶ��㣬��CM+MN����Сֵ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
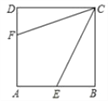
����Ŀ����ͼ��������ABCD�ı߳�Ϊ6����E��F�ֱ���AB��AD������CE=3![]() ���ҡ�ECF=45�㣬��CF��Ϊ�� ��
���ҡ�ECF=45�㣬��CF��Ϊ�� ��
A. 2![]() B. 3
B. 3![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������O���ڽ��ı���ABCD�У�AB=AD����C=120������E��![]() �ϣ�
�ϣ�
��1������E�Ķ�����
��2������OD��OE������DOE=90��ʱ��AEǡ��Ϊ��O���ڽ���n���ε�һ�ߣ���n��ֵ��
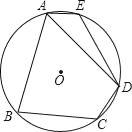
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+3��x���ཻ�ڵ�A����1��0����B��3��0������y���ཻ�ڵ�C����PΪ�߶�OB�ϵĶ��㣨����O��B�غϣ�������P��ֱ��x���ֱ�����������߶�BC�ֱ��ڵ�E��F����D��y���������ϣ�OD=2������DE��OF��
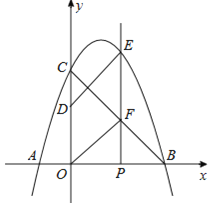
��1���������ߵĽ���ʽ��
��2�����ı���ODEF��ƽ���ı���ʱ�����P�����ꣻ
��3������A��ֱ�߽���2���е�ƽ���ı���ODEF�ֳ������ȵ������֣�������ֱ�ߵĽ���ʽ��������˵��ƽ��ƽ���ı�����������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���A=45�㣬AB=![]() ��AC=6����D��EΪ��AC�ϵĵ㣬AD=1��CE=2����FΪ�߶�DE��һ�㣨����D��E�غϣ����ֱ��Ե�D��EΪԲ�ģ�DF��EFΪ�뾶��Բ.����Բ���AB��BC������������ʱ���߶�DF���ȵ�ȡֵ��Χ��_______.
��AC=6����D��EΪ��AC�ϵĵ㣬AD=1��CE=2����FΪ�߶�DE��һ�㣨����D��E�غϣ����ֱ��Ե�D��EΪԲ�ģ�DF��EFΪ�뾶��Բ.����Բ���AB��BC������������ʱ���߶�DF���ȵ�ȡֵ��Χ��_______.
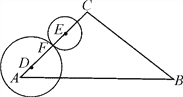
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�Ƶ���ŵ���ת���ڲ��������Ϊ2������Ϊ3�IJ���������������鲣���ڷ�ʱ�н���ͬ������ڴ���������֮��ľ���Ϊ2���������������е㵽����ת��˵ľ���Ϊ(����)

A. ![]() �� B. 2�� C. 2
�� B. 2�� C. 2![]() �� D. 3��
�� D. 3��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com