
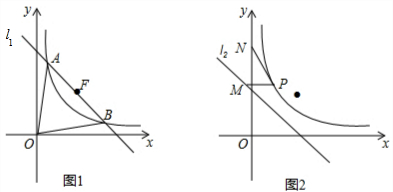
分析 (1)将l1与y=$\frac{1}{x}$组成方程组,即可得到C点坐标,从而求出△OAB的面积;
(2)根据题意得:$\left\{\begin{array}{l}{y-\sqrt{2}=k(x-\sqrt{2})}\\{y=\frac{1}{x}}\end{array}\right.$,整理得:kx2+$\sqrt{2}$(1-k)x-1=0(k<0),根据根与系数的关系得到2k2+5k+2=0,从而求出k的值;
(3)设P(x,$\frac{1}{x}$),则M(-$\frac{1}{x}$+$\sqrt{2}$,$\frac{1}{x}$),根据PM=PF,求出点P的坐标.
解答 解:(1)当k=-1时,l1:y=-x+2$\sqrt{2}$,
联立得$\left\{\begin{array}{l}{y=-x+2\sqrt{2}}\\{y=\frac{1}{x}}\end{array}\right.$,化简得x2-2$\sqrt{2}$x+1=0,
解得:x1=$\sqrt{2}$-1,x2=$\sqrt{2}$+1,
设直线l1与y轴交于点C,则C(0,2$\sqrt{2}$).
S△OAB=S△AOC-S△BOC=$\frac{1}{2}$×2$\sqrt{2}$(x2-x1)=2$\sqrt{2}$;
(2)根据题意得:$\left\{\begin{array}{l}{y-\sqrt{2}=k(x-\sqrt{2})}\\{y=\frac{1}{x}}\end{array}\right.$,
整理得:kx2+$\sqrt{2}$(1-k)x-1=0(k<0),
∵△=[$\sqrt{2}$(1-k)]2-4×k×(-1)=2(1+k2)>0,
∴x1、x2 是方程的两根,
∴$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=\frac{\sqrt{2}(k-1)}{k}}\\{{x}_{1}•{x}_{2}=-\frac{1}{k}}\end{array}\right.$,
∴AB2=(x1-x2)2+($\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$)2
=(x1-x2)2+($\frac{{x}_{2}-{x}_{1}}{{x}_{1}{x}_{2}}$)2
=(x1-x2)2[1+($\frac{1}{{x}_{1}{x}_{2}}$)2]
=$\frac{2(1+{k}^{2})^{2}}{{k}^{2}}$,
∴AB=-$\frac{-\sqrt{2}(1+{k}^{2})}{k}$=$\frac{5\sqrt{2}}{2}$,即$\frac{1+{k}^{2}}{k}$=$\frac{5}{2}$,
整理得,2k2+5k+2=0,即(2k+1)(k+1)=0,解得k=-1或k=-$\frac{1}{2}$.
(3)F($\sqrt{2}$,$\sqrt{2}$),如图: 设P(x,$\frac{1}{x}$),则M(-$\frac{1}{x}$+$\sqrt{2}$,$\frac{1}{x}$),
设P(x,$\frac{1}{x}$),则M(-$\frac{1}{x}$+$\sqrt{2}$,$\frac{1}{x}$),
则PM=x+$\frac{1}{x}$-$\sqrt{2}$=$\sqrt{(x+\frac{1}{x}-\sqrt{2})^{2}}$=$\sqrt{{x}^{2}+\frac{1}{{x}^{2}}-2\sqrt{2}(x+\frac{1}{x})+4}$,
∵PF=$\sqrt{(x-\sqrt{2})^{2}+(\frac{1}{x}-\sqrt{2})^{2}}$=$\sqrt{{x}^{2}+\frac{1}{{x}^{2}}-2\sqrt{2}(x+\frac{1}{x})+4}$,
∴PM=PF.
∴PM+PN=PF+PN≥NF=2,
当点P在NF上时等号成立,此时NF的方程为y=-x+2$\sqrt{2}$,
由(1)知P($\sqrt{2}$-1,$\sqrt{2}$+1),
∴当P($\sqrt{2}$-1,$\sqrt{2}$+1)时,PM+PN最小值是2.
点评 本题考查了反比例函数综合题,涉及函数图象的交点与方程组的解的关系、三角形的面积、一元二次方程根的判别式、一元二次方程的解法、两点间的距离公式等知识,综合性较强.


科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系内,函数y=$\frac{m}{x}$(x>0,m是常数)的图象经过点A(1,4),B(a,b)过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连结AD,CB,CD.
如图,在平面直角坐标系内,函数y=$\frac{m}{x}$(x>0,m是常数)的图象经过点A(1,4),B(a,b)过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连结AD,CB,CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知∠A,请你仅用没有刻度的直尺和圆规,按下列要求作图和计算(保留作图痕迹,不必写画法):
如图,已知∠A,请你仅用没有刻度的直尺和圆规,按下列要求作图和计算(保留作图痕迹,不必写画法):查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com