
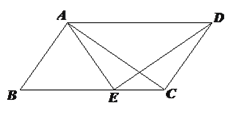
【题目】如图,在四边形ABCD中,AB//CD,∠B=∠ADC,点E是BC边上的一点,且AE=DC.
(1)求证:△ABC≌△EAD ;
(2)如果AB⊥AC,求证:∠BAE= 2∠ACB.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)易证△ABC≌△CDA得BC=AD,AB=DC,∠ACB=∠CAD;再证∠B=∠EAD;进而再证明AB=AE,即可得证;
(2)过点A作AH⊥BC于H ,利用等腰三角形的三线合一的性质和直角三角形两锐角互余即可得证.
试题解析:(1)∵ AB//CD,
∴ ∠BAC=∠DCA .
又 ∠B=∠ADC,AC=CA,
∴ △ABC≌△CDA .
∴ BC=AD,AB=DC,∠ACB=∠CAD .
又 AE=DC,AB=DC,
∴ AB=AE .
∴ ∠B=∠AEB .
又 ∠ACB=∠CAD,
∴ AD//BC,
∴ ∠AEB=∠EAD .
∴ ∠B=∠EAD .
在△ABC与△EAD中,
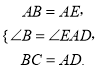
∴ △ABC≌△EAD .
(2)过点A作AH⊥BC于H .

∵ AB=AE,AH⊥BC .
∴ ∠BAE=2∠BAH .
在△ABC中,
∵ ∠BAC+∠B+∠ACB=180°,
又 AB⊥AC,∴ ∠BAC=90°.
∴ ∠B+∠ACB=90°.
同理:∠B+∠BAH=90°.
∴ ∠BAH=∠ACB .
∴ ∠BAE=2∠ACB .


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线y=3x+3与x轴交于点A,与x轴交于点B,过A,B两点的抛物线交x轴于另一点C(3,0).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△ABP是等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列数据是2015年某日发布的北京五个环境监测点PM2.5空气质量指数实时数据:
监测点 | A区 | B区 | C区 | D区 | E区 |
PM2.5指数 | 94 | 114 | 96 | 113 | 131 |
则这组数据的中位数是( )
A. 94 B. 96 C. 113 D. 113.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.
运用上述知识,解决下列问题:
(1)如果(a-2)![]() +b+3=0,其中a、b为有理数,那么a= ,b= ;
+b+3=0,其中a、b为有理数,那么a= ,b= ;
(2)如果(2+![]() )a-(1-
)a-(1-![]() )b=5,其中a、b为有理数,求a+2b的值.
)b=5,其中a、b为有理数,求a+2b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程kx2﹣3x﹣2=0有两个不相等的实数根.
(1)求k的取值范围;
(2)若k为小于2的整数,且方程的根都是整数,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
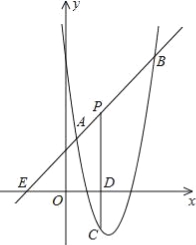
【题目】如图,直线y=x+2与抛物线y=![]() +bx+6(a≠0)相交于A(
+bx+6(a≠0)相交于A(![]() ,
,![]() )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)求△PAC为直角三角形时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com