
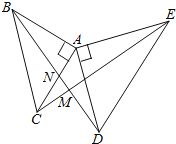
【题目】如图,△ABC和△ADE都是等腰直角三角形,CE与BD相交于点M,BD交AC于点N.
(1)证明:BD=CE;
(2)证明:BD⊥CE.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)要证明BD=CE,只要证明△ABD≌△ACE即可,两三角形中,已知的条件有AD=AE,AB=AC,那么只要再得出两对应边的夹角相等即可得出三角形全等的结论.我们发现∠BAD和∠EAC都是90°加上一个
∠CAD,因此∠CAE=∠BAD.由此构成了两三角形全等中的(SAS)因此两三角形全等.
(2)要证BD⊥CE,只要证明∠BMC是个直角就行了.由(1)得出的全等三角形我们可知:
∠ABN=∠ACE,三角形ABC中,∠ABN+∠CBN+∠BCN=90°,根据上面的相等角,我们可得出∠ACE+∠CBN+∠BCN=90°,即∠ABN+∠ACE=90°,因此∠BMC就是直角.
证明:(1)∵∠BAC=∠DAE=90°
∴∠BAC+∠CAD=∠DAE+∠CAD
即∠CAE=∠BAD
在△ABD和△ACE中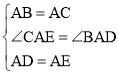
∴△ABD≌△ACE(SAS)
∴BD=CE
(2)∵△ABD≌△ACE
∴∠ABN=∠ACE
∵∠ANB=∠CND
∴∠ABN+∠ANB=∠CND+∠NCE=90°
∴∠CMN=90°
即BD⊥CE.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
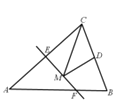
【题目】如图,等腰三角形ABC的底边BC长为6,面积是36,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】意大利文艺复兴时期的著名画家达芬奇利用两张一样的纸片拼出不一样的“空洞”,从而巧妙的证明了勾股定理.小明用两张全等的的纸片①和②拼成如图1所示的图形,中间的六边形![]() 由两个正方形和两个全等的直角三角形组成.已知六边形
由两个正方形和两个全等的直角三角形组成.已知六边形![]() 的面积为28,
的面积为28,![]() .小明将纸片②翻转后拼成如图2所示的图形,其中
.小明将纸片②翻转后拼成如图2所示的图形,其中![]() ,则四边形
,则四边形![]() 的面积为( )
的面积为( )

A.16B.20C.22D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
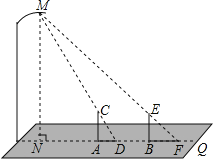
【题目】晚饭后,小林和小京在社区广场散步,两人在灯下沿直线NQ移动,如图,当小林正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小京正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小林的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小京身高BE的长.(结果精确到0.01米)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com