
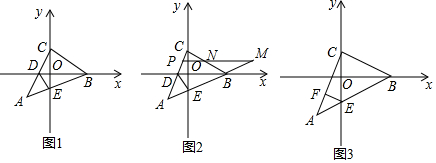
分析 (1)如图1中,作AF⊥y轴于F,只要证明△ACF≌△CBO,可得AF=OC,CF=OB,由A(-1,-1),推出AF=OF=OC=1,OB=CF=2,由此即可解决问题.
(2)如图1中,将△AEF绕点A逆时针旋转90°得到△AMN,只要证明△DAN≌△DAE,可得∠ADN=∠ADE,由∠ADN=∠CDB,推出∠CDB=∠ADE.
(3)由题意直线AC的解析式为y=2x+1,设P(m,2m+1),想办法求出点M、N的坐标,求出PN、PM即可解决问题.
(4)求出点E坐标,求出AE、AB、BC,根据EF∥BC,得$\frac{EF}{BC}$=$\frac{AE}{AB}$,即可解决问题.
解答 (1)解:如图1中,作AF⊥y轴于F,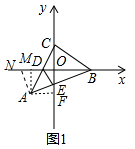
∵∠ACB=∠AFC=∠BOC=90°,
∴∠ACF+∠BCO=90°,∠CAF+∠ACF=90°,
∴∠BCO=∠CAF,
在△ACF和△BCO中,
$\left\{\begin{array}{l}{∠CAF=∠BCO}\\{∠AFC=∠BOC}\\{AC=BC}\end{array}\right.$,
∴△ACF≌△CBO,
∴AF=OC,CF=OB,
∵A(-1,-1),
∴AF=OF=OC=1,OB=CF=2,
∴B(2,0).
(2)如图1中,将△AEF绕点A逆时针旋转90°得到△AMN,
∵∠AMO=∠AFO=∠MOF=90°,
∴四边形AMOF是矩形,
∵AM=AF,
∴四边形AMOF是正方形,
∵∠CAB=45°,
∴∠EAF+∠MAD=45°=∠NAM+∠MAD=∠NAD,
∴∠NAD=∠EAD,
在△ADN和△ADE中,
$\left\{\begin{array}{l}{AD=AD}\\{∠DAN=∠DAE}\\{AN=AE}\end{array}\right.$,
∵△DAN≌△DAE,
∴∠ADN=∠ADE,
∵∠ADN=∠CDB,
∴∠CDB=∠ADE.
(3)如图2中,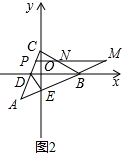
∵A(-1,-1),C(0,1),
∴直线AC的解析式为y=2x+1,设P(m,2m+1),
∵C(0,1),B(2,0),
∴直线BC的解析式为y=-$\frac{1}{2}$x+1,
∵PM∥x轴,
∴点N与点P的纵坐标相同,2m+1=-$\frac{1}{2}$x+1,
∴x=-4m,
∴N(-4m,2m+1),
∵A(-1,-1),B(2,0),
∴直线AB的解析式为y=$\frac{1}{3}$x-$\frac{2}{3}$,
∵PM∥x轴,
∴点M与点P的纵坐标相同,2m+1=$\frac{1}{3}$x-$\frac{2}{3}$,
∴x=6m+5,
∴M(6m+5,2m+1),
∴PN=-5m,PM=5m+5,
∴PN+PM=-5m+5m+5=5.
(4)如图3中,
由(3)可知,直线AB的解析式为y=$\frac{1}{3}$x-$\frac{2}{3}$,
∴E(0,-$\frac{2}{3}$),
∵A(-1,-1),B(2,0),C(0,1),
∴AE=$\sqrt{{1}^{2}+(\frac{1}{3})^{2}}$=$\frac{\sqrt{10}}{3}$,AB=$\sqrt{10}$,BC=$\sqrt{5}$,
∵EF∥BC,
∴$\frac{EF}{BC}$=$\frac{AE}{AB}$,
∴$\frac{EF}{\sqrt{5}}$=$\frac{\frac{\sqrt{10}}{3}}{\sqrt{10}}$,
∴EF=$\frac{\sqrt{5}}{3}$.
点评 本题考查三角形综合题、全等三角形的判定和性质、等腰直角三角形的性质、一次函数的应用、平行线分线段成比例定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形,学会利用一次函数求交点坐标,属于中考压轴题.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
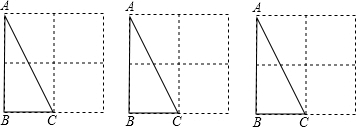
 已知:如图,在山脚的C处测得山顶A的仰角为53°,沿着坡度为30°的斜坡前进400米到D处(即∠DCB=30°,CD=400米),测得A的仰角为63°,求此山的高度AB.(答案保留根号)
已知:如图,在山脚的C处测得山顶A的仰角为53°,沿着坡度为30°的斜坡前进400米到D处(即∠DCB=30°,CD=400米),测得A的仰角为63°,求此山的高度AB.(答案保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com