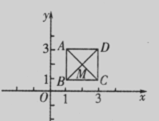
如图，已知正方形ABCD，顶点A(1，3)、B(1,1)、C(3,1)．规定“把正方形ABCD先沿x轴翻折，再向左平移1个单位”为一次变换．如此这样，连续经过2014次变换后，正方形ABCD的对角线交点M的坐标变为 ( )
A．(—2012,2) B．（一2012，一2）
C. (—2013,—2) D. (—2013,2)
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目：初中数学 来源： 题型：
大学生小张利用暑假50天在一超市勤工俭学，被安排销售一款成本为40元/件的新型商品，此类新型商品在第x天的销售量p件与销售的天数x的关系如下表：
| x(天) | 1 | 2 | 3 | … | 50 |
| p(件) | 118 | 116 | 114 | … | 20 |
销售单价q(元/件)与x满足:当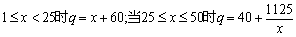
.
（1）（2分）请分析表格中销售量p与x的关系，求出销售量p与x的函数关系.
（2）（4分）求该超市销售该新商品第x天获得的利润y元关于x的函数关系式.
（3）（4分）这50天中，该超市第几天获得利润最大？最大利润为多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
鸡兔同笼”问题：
《孙子算经》是唐初作为“算学”教科书的著名的《算经十书》之一，共三卷，上卷叙述算筹记数的制度和乘除法则，中卷举例说明筹算分数法和开平方法，都是了解中国古代筹算的重要资料。下卷收集了一些算术难题，“鸡兔同笼”问题是其中之一。原题如下： 令有雉（鸡）兔同笼，上有三十五头，下有九十四足。 则鸡有 12 只，兔有 22 只。
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，某水平地面上建筑物的高度为AB，在点D和点F处分别竖立高是2米的CD和EF，两标杆相隔52米，并且建筑物AB、标杆CD和EF在同一竖直平面内，从标杆CD后退2米到点G处，在G处测得建筑物顶端A和标杆顶端C在同一条直线上；从标杆FE后退4米到点H处，在H处测得建筑物顶端A和标杆顶端E在同一条直线上，则建筑物的高是 米．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，抛物线y=ax2+bx+c（a≠O）与y轴交于点C(O，4)，与x轴交于点A和点B，其中点A的坐标为（-2,0），抛物线的对称轴x=1与抛物线交于点D，与直线BC交于点E
(1)求抛物线的解析式；
(2)若点F是直线BC上方的抛物线上的一个动点，是否存在点F使四边形ABFC的面积为17，若存在，求出点F的坐标；若不存在，请说明理由；
(3)平行于DE的一条动直线Z
与直线BC相交于点P，与抛物线相交于点Q，若以D、E、P、Q为顶点的四边形是平行四边形，求点P的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
无解，则实数a的取值范围是( )
，以点B为圆心，BC长为半径画弧，交边AD于点E，若AE·ED＝
，则矩形ABCD的面积为 ．
有意义，则实数x的取值范围是