
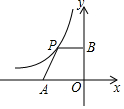
 如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数y=$\frac{-6}{x}$(x<0)上一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数y=$\frac{-6}{x}$(x<0)上一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )| A. | 先增后减 | B. | 先减后增 | C. | 逐渐减小 | D. | 逐渐增大 |
分析 过点P作PC⊥x轴于点C,根据k的几何意义可知矩形PBOC的面积为6,然后只需要讨论△APC的面积大小即可.
解答 解: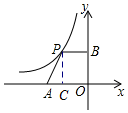 过点P作PC⊥x轴于点C,
过点P作PC⊥x轴于点C,
∵点P在y=-$\frac{6}{x}$(x<0)
∴矩形PBOC的面积为6
设A的坐标为(a,0),P坐标(x,$-\frac{6}{x}$)(x<0),
△APC的面积为S,
当a<x<0时,
∴AC=x-a,
∴PC=-$\frac{6}{x}$
∴△APC的面积为S=$\frac{1}{2}$(x-a)•$\frac{-6}{x}$=-3(1-$\frac{a}{x}$)
∵a<0,
∴-a>0,
∴-$\frac{a}{x}$在a<x<0上随着x的增大而减小,
∴1-$\frac{a}{x}$在a<x<0上随着x的增大而减小,
∴-3(1-$\frac{a}{x}$)在a<x<0上随着x的增大而增大,
∴S=S△APC+6
∴S在a<x<0上随着x的增大而增大,
当x≤a时,
∴AC=a-x,
∴PC=-$\frac{6}{x}$
∴△APC的面积为S=$\frac{1}{2}$(a-x)•$\frac{-6}{x}$=-3($\frac{a}{x}$-1)
∵a<0,
∴$\frac{a}{x}$在x<a随着x的增大而增大,
∴$\frac{a}{x}$-1在x<a上随着x的增大而增大,
∴-3($\frac{a}{x}$-1)在x<a上随着x的增大而减小,
∴S=6-S△APC
∴S在x<a上随着x的增大而增大,
∴当P的横坐标增大时,S的值是逐渐增大,
故选(D)
点评 本题考查反比例函数的图象性质,解题的关键是将点P的位置分为两种情况进行讨论,然后根据反比例函数的变化趋势求出△APC的面积变化趋势.本题综合程度较高.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
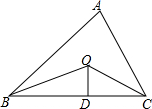 如图,已知△ABC的周长是29,OB,OC分别平分∠ABC和∠ACB,OD⊥BC,垂足为D,且OD=3,则△ABC的面积是$\frac{87}{2}$.
如图,已知△ABC的周长是29,OB,OC分别平分∠ABC和∠ACB,OD⊥BC,垂足为D,且OD=3,则△ABC的面积是$\frac{87}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 班级 | 考试人数 | 平均分 | 中位数 | 众数 | 方差 |
| 一班 | 51 | 80 | 84 | 88.78 | 186 |
| 二班 | 51 | 80 | 86 | 78 | 161 |
| A. | 一班、二班学生成绩的平均数相同 | |
| B. | 二班优生多于一班(优生为85分或85分以上者) | |
| C. | 二班成绩比一班整齐 | |
| D. | 成绩为78分的学生二班比一班多 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com