
【题目】已知抛物线y=ax2﹣2ax﹣3a与y轴交于C点,交x轴于A、B,且OB=OC.
(1)求抛物线的解析式;
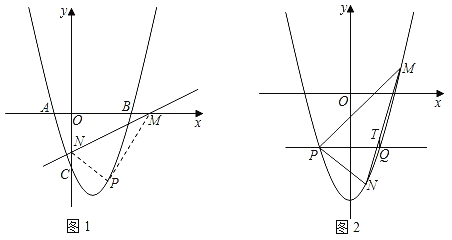
(2)如图1,直线l:y=![]() x+b(b<0)交x轴于M,交y轴于N.将△MON沿直线l翻折,得到△MPN,点O的对应点为P.若O的对应点P恰好落在抛物线上,求直线l的解析式;
x+b(b<0)交x轴于M,交y轴于N.将△MON沿直线l翻折,得到△MPN,点O的对应点为P.若O的对应点P恰好落在抛物线上,求直线l的解析式;
(3)如图2,将原抛物线向左平移1个单位,向下平移t个单位,得到新抛物线C1.若直线y=m与新抛物线C1交于P、Q两点,点M是新抛物线C1上一动点,连接PM,并将直线PM沿y=m翻折交新抛物线C1于N,过Q作QT∥y轴,交MN于点T,求![]() 的值.
的值.
【答案】(1)抛物线的表达式为y=x2﹣2x﹣3;(2)直线l的表达式为:y=![]() x﹣
x﹣![]() ;(3)1.
;(3)1.
【解析】
(1)OB=OC=3a,故点B(3a,0),将点B的坐标代入y=ax22ax3a,即可求解;
(2)求出点P的坐标(﹣![]() b,
b,![]() b),将点P的坐标代入抛物线表达式,即可求解;
b),将点P的坐标代入抛物线表达式,即可求解;
(3)计算xP+xM=k,同理可得:xP+xN=﹣k,而xT=xQ=﹣xP,而TH∥MG,故![]() ,即
,即![]() =
=![]() =1.
=1.
解:(1)∵c=﹣3a,
∴OB=OC=3a,故点B(3a,0),
将点B的坐标代入y=ax2﹣2ax﹣3a并解得:a=1或﹣![]() (舍去﹣
(舍去﹣![]() ),
),
故抛物线的表达式为:y=x2﹣2x﹣3;

(2)连接OP,交MN于点K,则OP⊥MN,
则直线OP的表达式为:y=﹣2x,而直线MN的表达式为:y=![]() x+b,
x+b,
联立上述两个表达式并解得:x=﹣![]() b,则点K(﹣
b,则点K(﹣![]() b,
b,![]() b),
b),
∵点K是OP的中点,由中点公式得:点P的坐标为(﹣![]() b,
b,![]() b),
b),
将点P的坐标代入抛物线表达式得:(﹣![]() b)2﹣2(﹣
b)2﹣2(﹣![]() b)﹣3=
b)﹣3=![]() b,解得:b=﹣
b,解得:b=﹣![]()
(不合题意值已舍去);
故直线l的表达式为: y=![]() x﹣
x﹣![]() ;
;
(3)平移后抛物线的表达式C1:y=x2﹣4﹣t①,
设直线PM的表达式为:y=kx+c②;则PN的表达式为:y=﹣kx+d,
联立①②并整理得:x2﹣kx﹣(4+t+c)=0,
∴xP+xM=k,
同理可得:xP+xN=﹣k,而xT=xQ=﹣xP,
如图2,过点N作x轴的平行线交过点M与y轴的平行线于点G,延长TQ交NG于点H,

∴TH∥MG,故![]() ,即
,即![]() =
=![]() =1.
=1.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在0,3.14,![]() ,2π,-
,2π,-![]() ,
,![]() ,-0.4,-
,-0.4,-![]() ,4.262262226…(每两个”6”之间依次多一个”2”)中,
,4.262262226…(每两个”6”之间依次多一个”2”)中,
属于有理数的有_________________________________________________;
属于无理数的有________________________________________________________;
属于正实数的有_________________________________________________________;
属于负实数的有_____________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇同学用配方法推导一元二次方程ax2+bx+c=0(a≠0)的求根公式时,对于b2﹣4ac>0的情况,她是这样做的:
由于a≠0,方程ax2+bx+c=0变形为:
x2+![]() x=﹣
x=﹣![]() ,…第一步
,…第一步
x2+![]() x+(
x+(![]() )2=﹣
)2=﹣![]() +(
+(![]() )2,…第二步
)2,…第二步
(x+![]() )2=
)2=![]() ,…第三步
,…第三步
x+![]() =
=![]() (b2﹣4ac>0),…第四步
(b2﹣4ac>0),…第四步
x=![]() ,…第五步
,…第五步
嘉淇的解法从第 步开始出现错误;事实上,当b2﹣4ac>0时,方程ax2+bx+c=0(a≠O)的求根公式是 .
用配方法解方程:x2﹣2x﹣24=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在数轴上A点表示数![]() ,B点表示数
,B点表示数![]() ,
,![]() 、
、![]() 满足|
满足|![]() |+|
|+|![]() |=0;
|=0;
![]()
(1)点A表示的数为_____;点B表示的数为_____;
(2)若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),
①当t=1时,甲小球到原点的距离=_____;乙小球到原点的距离=_____.
当t=3时,甲小球到原点的距离=_____;乙小球到原点的距离=_____.
②试探究:甲,乙两小球到原点的距离可能相等吗?若不能,请说明理由.若能,请直接写出甲,乙两小球到原点的距离相等时经历的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列10×10的网格中,横、纵坐标均为整点的数叫做格点,例如A(﹣2,﹣2)、B(5,﹣3)、C(1,1)都是格点.
(1)∠ACB的大小为 ;
(2)要求在下图中仅用无刻度的直尺作图:以A为中心,取旋转角等于∠BAC.把△ABC逆时针旋转,得到△AB1C1,其中点C和点B的对应点分别为点C1和点B1,操作步骤如下:
第一步:延长AC到格点B1,使得AB1=AB;
第二步:延长BC到格点E,使得CE=CB,连接AE;
第三步:取格点F,连接FB1交AE于点C1,则△AB1C1即为所求.
请你按步骤完成作图,并直接写出B1、E、F三点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的边AB是⊙O的弦.
(1)如图1,若AB是⊙O的直径,AB=AC,BC交⊙O于点D,且DM⊥AC于M,请判断直线DM与⊙O的位置关系,并给出证明;
(2)如图2,AC交⊙O于点E,若E恰好是![]() 的中点,点E到AB的距离是8,且AB长为24,求⊙O的半径长.
的中点,点E到AB的距离是8,且AB长为24,求⊙O的半径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于受到手机更新换代的影响,某手机店经销的甲型号手机二月份售价比一月份售价每台降价500元.如果卖出相同数量的手机,那么一月份销售额为9万元,二月份销售额只有8万元.
(1)求二月份甲型号手机每台售价为多少元?
(2)为了提高利润,该店计划三月份加入乙型号手机销售,已知甲型每台进价为3500元,乙型每台进价为4000元,预计用不多于7.6万元且不少于7.5万元的资金购进这两种手机共20台,请问有几种进货方案?
(3)对于(2)中刚进货的20台两种型号的手机,该店计划对甲型号手机在二月份售价基础上每售出一台甲型手机再返还顾客现金a元,乙型手机按销售价4400元销售,若要使(2)中所有方案获利相同,a应取何值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com