
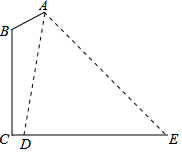
 如图,在路边安装路灯,灯柱BC高15m,与灯杆AB的夹角ABC为120°.路灯采用锥形灯罩,照射范围DE长为18.9m,从D、E两处测得路灯A的仰角分别为∠ADE=80.5°,∠AED=45°.求灯杆AB的长度.(参考数据:cos80.5°≈0.2,tan80.5°≈6.0)
如图,在路边安装路灯,灯柱BC高15m,与灯杆AB的夹角ABC为120°.路灯采用锥形灯罩,照射范围DE长为18.9m,从D、E两处测得路灯A的仰角分别为∠ADE=80.5°,∠AED=45°.求灯杆AB的长度.(参考数据:cos80.5°≈0.2,tan80.5°≈6.0) 分析 过点A作AF⊥CE,点B作BG⊥AF,根据正切的概念求出DF,列方程求出AF,根据正弦的概念计算即可.
解答 解:过点A作AF⊥CE,交CE于点F.
设AF的长度为xm.
∵∠AED=45°,
∴△AEF是等腰直角三角形.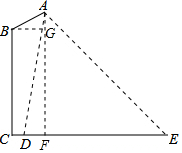
∴EF=AF=x.
在Rt△ADF中,∵tan∠ADF=$\frac{AF}{DF}$,
∴DF=$\frac{AF}{tan∠ADF}$=$\frac{x}{tan80.5°}$=$\frac{x}{6}$.
∵DE=18.9,
∴$\frac{x}{6}$+x=18.9,
解得x=16.2,
过点B作BG⊥AF,交AF于点G,
则BC=GF=15,∠CBG=90°.
∴AG=AF-GF=16.2-15=1.2,
∵∠ABC=120°,
∴∠ABG=∠ABC-∠CBG=120°-90°=30°.
在Rt△ABG中,
∵sin∠ABG=$\frac{AG}{AB}$,
∴AB=$\frac{AG}{sin∠ABG}$=$\frac{1.2}{sin30°}$=2.4,
答:灯杆AB的长度为2.4 m.
点评 本题考查的是解直角三角形的应-仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
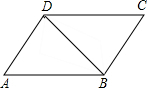 如图,已知AD∥CB,∠A=∠C,若∠ABD=32°,求∠BDC的度数.有同学用了下面的方法.但由于一时犯急没有写完整,请你帮他添写完整.
如图,已知AD∥CB,∠A=∠C,若∠ABD=32°,求∠BDC的度数.有同学用了下面的方法.但由于一时犯急没有写完整,请你帮他添写完整.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com