练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】把下列角度化成以度表示的形式．

    (1)15°24′36″；　(2)36°59′96″；　(3)50°65′60″.

    【答案】（1）15.41°.（2）37.01°.（3）51.1°.

    【解析】（1）先把36″化成分，再把（24+0.6）′化成度，即可得出答案；

    （2）先把96″化成分，再把（59+1.6）′化成度，即可得出答案；

    （3）先把60″化成分，再把（65+1）′化成度，即可得出答案．

    (1)15°24′36″＝15°24′＋′＝15°24.6′＝15°＋°＝15.41°.

    (2)36°59′96″＝36°＋1°＋′＝37°＋0.6′＝37°＋°＝37.01°.

    (3)50°65′60″＝50°66′＝51°6′＝51°＋°＝51.1°.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在数学活动课上，老师要求学生在5×5的正方形ABCD网格中（小正方形的边长为1）画直角三角形，要求三个顶点都在格点上，而且三边与AB或AD都不平行．画四种图形，并直接写出其周长（所画图象相似的只算一种）．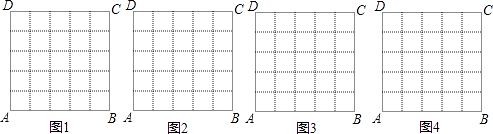

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：

    (1)(－15)÷(－3)；

    (2)(－12)÷(－)；

    (3)(－0.75)÷0.25；

    (4)(－12)÷(－)÷(－100)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y=ax2+bx+c（a≠0）的顶点坐标为Q（2，﹣1），且与y轴交于点C（0，3），与x轴交于A，B两点（点A在点B的右侧），点P是该抛物线上的一动点，从点C沿抛物线向点A运动（点P与A不重合），过点P作PD∥y轴，交AC于点D．

    （1）求该抛物线的函数关系式；
    （2）当△ADP是直角三角形时，求点P的坐标；
    （3）在题（2）的结论下，若点E在x轴上，点F在抛物线上，问是否存在以A、P、E、F为顶点的平行四边形？若存在，求点F的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的边长为1，AC，BD是对角线。将△DCB绕着点D顺时针旋转45°得到△DGH，HG交AB于点E，连接DE交AC于点F，连接FG。则下列结论：

    ①四边形AEGF是菱形 ②△AED≌△GED

    ③∠DFG=112.5° ④BC+FG=1.5

    其中正确的结论是（ ）

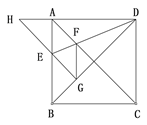
    A. ①②③④ B. ①②③ C. ①② D. ②

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：线段AB=20cm．

    （1）如图1，点P沿线段AB自A点向B点以2厘米/秒运动，点P出发2秒后，点Q沿线段BA自B点向A点以3厘米/秒运动，问再经过几秒后P、Q相距5cm?

    （2）如图2：AO=4厘米，PO=2厘米，∠POB=60°，点P绕着点O以60°/秒的速度逆时针旋转一周停止，同时点Q沿直线BA自B点向A点运动，假若点P、Q两点能相遇，求点Q运动的速度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知正方形ABCD的对角线AC、BD相交于点O，E是AC上一点，过点A作AG⊥EB，垂足为G，AG交BD于F，则OE=OF．

    （1）请证明0E=OF

    （2）解答（1）题后，某同学产生了如下猜测：对上述命题，若点E在AC的延长线上，AG⊥EB，AG交 EB的延长线于 G，AG的延长线交DB的延长线于点F，其他条件不变，则仍有OE=OF．问：猜测所得结论是否成立？若成立，请给出证明；若不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB＝AC，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别为E，F，则下列四个结论：①AD上任意一点到点C，B的距离相等；②AD上任意一点到AB，AC的距离相等；③BD＝CD，AD⊥BC；④∠BDE＝∠CDF.其中正确的个数是(　　)

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，已知点A（﹣3，0）、B（0，4），对△OAB连续作旋转变换，依次得到△1、△2、△3、△4…，则△2016的直角坐标顶点的坐标为（ ）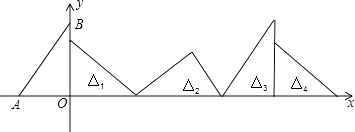

    A.（8053，0）
    B.（8064，0）
    C.（8053， ）
    D.（8064， ）

    查看答案和解析>>

    同步练习册答案