

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 21 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 21 |
| 2 |
| 1 |
| 2 |
| 21 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 21 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 21 |
| 2 |
| 1 |
| 2 |
| 21 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
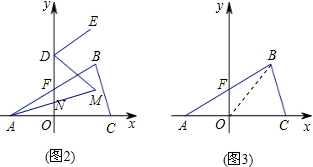
 如图是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )
如图是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )| A、a2+b2 |
| B、4ab |
| C、(b+a)2-4ab |
| D、b2-a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
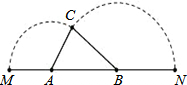 如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC.设AB=x,若△ABC为直角三角形,则x=
如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC.设AB=x,若△ABC为直角三角形,则x=查看答案和解析>>
科目:初中数学 来源: 题型:
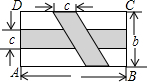 如图,在矩形ABCD中,横向阴影部分是矩形,另一阴影部分是平行四边形.依照图中标注的数据,计算图中空白部分的面积,已知a=2b=6c,其面积是
如图,在矩形ABCD中,横向阴影部分是矩形,另一阴影部分是平行四边形.依照图中标注的数据,计算图中空白部分的面积,已知a=2b=6c,其面积是查看答案和解析>>
科目:初中数学 来源: 题型:
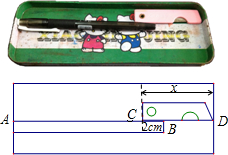 如图,在铅笔盒中有一支圆珠笔和一把小刀,已知圆珠笔的长AB是小刀长CD(小刀不打开时的最大长度)的
如图,在铅笔盒中有一支圆珠笔和一把小刀,已知圆珠笔的长AB是小刀长CD(小刀不打开时的最大长度)的| 15 |
| 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:
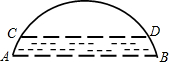 如图是一座桥其中一个拱洞的简易图形,最初的水位在AB处,此时水面宽60米,拱高(拱弧
如图是一座桥其中一个拱洞的简易图形,最初的水位在AB处,此时水面宽60米,拱高(拱弧 |
| AB |
查看答案和解析>>
科目:初中数学 来源: 题型:
| π |
| 2 |
| 1 |
| 8 |
| .. |
| 56 |
| 9 |
| 3 | -8 |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、甲站东边25m处 |
| B、甲站西边25m处 |
| C、甲站东边85m处 |
| D、甲站西边55m处 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com