
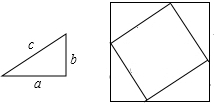

 ab,
ab, ab,
ab,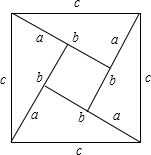
 ab×4+(b-a)2,
ab×4+(b-a)2, b×4+(b-a)2,c2=2ab+b2-2ab+a2,
b×4+(b-a)2,c2=2ab+b2-2ab+a2,

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:非常讲解·教材全解全析数学八年级上(配课标北师大版) 课标北师大版 题型:047
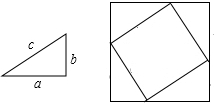
现有四块直角边为a、b,斜边为c的直角三角形的纸板,请从中取出若干块拼图(需画出所拼的图形)证明勾股定理.
查看答案和解析>>
科目:初中数学 来源:新课标三维目标导学与测评 数学八年级上册 题型:047
现有四块直角边为a,b,斜边为c的直角三角形纸板,请从中取出若干块拼图(需画出所拼图形),证明勾股定理.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com