
【题目】如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若C在线段AB的延长线上,且满足AC﹣BC=b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?并说明理由;
![]()
【答案】(1)线段MN的长是7cm;(2)线段MN的长是![]() acm;(3)线段MN的长是
acm;(3)线段MN的长是![]() bcm.
bcm.
【解析】试题分析:(1)先由点M、N分别是AC、BC的中点得出MC=4cm,NC=3cm,再运用MN=MC+CN即可求解;
(2)与(1)的过程类似,即可得出相应的结论;
(3)先根据题意画出图形,再运用MN=MC-CN=![]() (AC-BC)即可求解.
(AC-BC)即可求解.
试题解析:(1)∵点M、N分别是AC、BC的中点,
∴MC=![]() AC=
AC=![]() ×8=4(cm),NC=
×8=4(cm),NC=![]() BC=
BC=![]() ×6=3(cm),
×6=3(cm),
∴MN=MC+CN=4+3=7(cm);
(2)MN=![]() a.理由如下:
a.理由如下:
∵点M、N分别是AC、BC的中点,
∴MC=![]() AC,NC=
AC,NC=![]() BC,
BC,
∴MN=MC+CN=![]() (AC+BC)=
(AC+BC)= ![]() a(cm);
a(cm);
(3)如图:
![]()
∵点M、N分别是AC、BC的中点,
∴MC=![]() AC,NC=
AC,NC=![]() BC,
BC,
∴MN=MC-CN=![]() (AC-BC)=
(AC-BC)= ![]() b(cm).
b(cm).


科目:初中数学 来源: 题型:
【题目】学习了有理数的乘法后,老师给同学们布置这样一道题目:计算49![]() ×(–5),看谁算的又快又对,有三位同学的解法如下:
×(–5),看谁算的又快又对,有三位同学的解法如下:
小军:原式 =(49 + ![]() )×(–5)= 49×(–5)+
)×(–5)= 49×(–5)+ ![]() ×(–5)
×(–5)
=–245–4![]() =–249
=–249![]() ;
;
小明:原式 = –![]() × 5 = –
× 5 = –![]() = – 249
= – 249 ![]() ;
;
小丽:原式 =(49 + ![]() )×(-5)=(50 -1 +
)×(-5)=(50 -1 + ![]() )×(-5)
)×(-5)
=(50 - ![]() )×(-5)= 50 ×(-5)+( -
)×(-5)= 50 ×(-5)+( - ![]() ) ×(-5)
) ×(-5)
= –250 +![]() = –249
= –249![]() ;
;
(1)对于以上三种解法,你认为谁的解法较好?
(2)上面的解法对你有何启发,用你认为最合适的方法计算:
19![]() ×(– 8)
×(– 8)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小彬和小明每天早晨坚持跑步,小彬每秒跑4米,小明每秒跑6米.
(1)如果他们站在百米跑道的两端同时相向起跑,那么几秒后两人相遇?
(2)如果小明站在百米跑道的起点处,小彬站在他前面10米处,两人同时同向起跑,几秒后小明能追上小彬?
(2)如果他们都站在四百米环形跑道的起点处,两人同时同向起跑,几分钟后他们再次相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
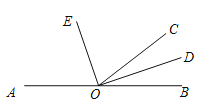
【题目】如图,已知点O是直线AB上的一点, ![]() ,OD、OE分别是
,OD、OE分别是![]() 、
、![]() 的角平分线.
的角平分线.
(1)求![]() 的度数;
的度数;
(2)写出图中与![]() 互余的角;
互余的角;
(3)图中有![]() 的补角吗?若有,请把它找出来,并说明理由.
的补角吗?若有,请把它找出来,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是( ) 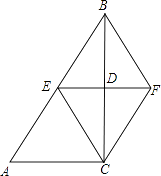
A.BC=AC
B.CF⊥BF
C.BD=DF
D.AC=BF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列算式:12-02=1+0=1,,22-12=2+1=3,32-22=3+2=5,42-32=4+3=7 ,52-42=5+4=9,…….
若字母 ![]() 表示自然数,请把你观察到的规律用含有
表示自然数,请把你观察到的规律用含有 ![]() 的式子表示出来________.
的式子表示出来________.
查看答案和解析>>
科目:初中数学 来源: 题型:
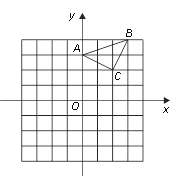
【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中, 每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比为2︰1,并直接写出C2点的坐标及△A2BC2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,不能判断四边形ABCD是平行四边形的是( )
A.∠A=∠C,∠B=∠D
B.AB∥CD,AB=CD
C.AB=CD,AD∥BC
D.AB∥CD,AD∥BC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com