
分析 (1)根据图象上的点满足函数解析式,可得b=2a+$\frac{1}{2}$c,根据根的判别式,可得答案;
(2)根据图象上的点满足函数解析式,可得关于b的方程,根据解方程,可得答案;
(3)根据待定系数法,可得函数解析式,根据相似三角形的判定与性质,可得关于n的方程,根据解方程,可得答案.
解答 (1)证明:由图象L经过点A(-2,0,得
4a-2b+c=0,
∴b=2a+$\frac{1}{2}$c.
∴b2-4ac=(2a+$\frac{1}{2}$c)2-4ac=(2a-$\frac{1}{2}$c)2.
∵c≠4a,
∴2a-$\frac{1}{2}$c≠0,
∴(2a-$\frac{1}{2}$c)2>0,即b2-4ac>0.
(2)解:∵点B(-$\frac{c}{2a}$,b+3)在图象L上,
∴$a•\frac{c^2}{{4{a^2}}}+b•(-\frac{c}{2a})+c=b+3$,整理,得
$\frac{c(4a-2b+c)}{4a}=b+3$.
∵4a-2b+c=0,
∴b+3=0,解得
b=-3.
(3)解:由题意,得$-\frac{-3}{2a}=3$,且36a-18+c=-8,解得a=$\frac{1}{2}$,c=-8.
∴图象L的解析式为y=$\frac{1}{2}$x2-3x-8.
设OC与对称轴交于点Q,图象L与y轴相交于点P,
则Q(3,-4),P(0,-8),OQ=PQ=5.
分两种情况:①当OD=OE时,如图1,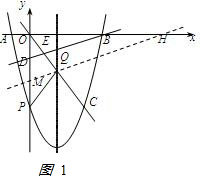 ,
,
过点Q作直线MQ∥DB,交y轴于点M,交x轴于点H,
则$\frac{OM}{OD}=\frac{OQ}{OE}$,
∴OM=OQ=5.
∴点M的坐标为(0,-5).
设直线MQ的解析式为y=k1x-5.
∵MQ经过点Q(3,-4),
∴3k1-5=-4,解得
${k_1}=\frac{1}{3}$.
∴MQ的解析式为$y=\frac{1}{3}x-5$.
易得点H(15,0).
又∵MH∥DB,
$\frac{OD}{OM}=\frac{OB}{OH}$.
即$\frac{-n}{5}=\frac{8}{15}$,
∴$n=-\frac{8}{3}$.
②当EO=ED时,如图2,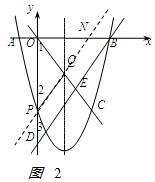 ,
,
∵OQ=PQ,
∴∠1=∠2,又EO=ED,
∴∠1=∠3
∴∠2=∠3,
∴PQ∥DB.
设直线PQ交于点N,其函数表达式为y=k2x-8
∴3k2-8=-4,解得${k_2}=\frac{4}{3}$.
∴PQ的解析式为$y=\frac{4}{3}x-8$.
∴点N的坐标为(6,0).
∵PN∥DB,
∴$\frac{OD}{OP}=\frac{OB}{ON}$,
∴$\frac{-n}{8}=\frac{8}{6}$,解得$n=-\frac{32}{3}$.
综上所述,当△ODE是等腰三角形时,n的值为$-\frac{8}{3}$或$-\frac{32}{3}$.
点评 本题考查了二次函数综合题,解(1)的关键是利用根的判别式;解(2)的关键是利用图象上的点满足函数解析式得出关于b的方程;解(3)的关键是利用相似三角形的判定与性质得出关于n的方程,要分类讨论,以防遗漏.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:选择题
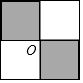 定义:用形状、大小完全相同的一种或几种平面图进行拼接,彼此之间不留空隙,不重叠地铺成一片,称为平面图形的镶嵌,如图是只选用大小相同的正方形在某顶点O周围拼接成的镶嵌图案.判断:若只选用一种大小相同的正多边形,在下列四个选项中,能进行平面镶嵌的是( )
定义:用形状、大小完全相同的一种或几种平面图进行拼接,彼此之间不留空隙,不重叠地铺成一片,称为平面图形的镶嵌,如图是只选用大小相同的正方形在某顶点O周围拼接成的镶嵌图案.判断:若只选用一种大小相同的正多边形,在下列四个选项中,能进行平面镶嵌的是( )| A. | 正五角形 | B. | 正六边形 | C. | 正八边形 | D. | 正十边形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
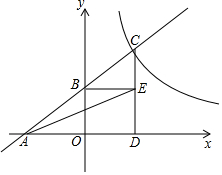 如图,直线AB与x轴交于点A,与y轴交于点B,与双曲线y=$\frac{k}{x}$(k>0)交于点C,过点C作CD⊥x轴于点D,过点B作BE⊥CD于点E,tan∠BCE=$\frac{3}{2}$,点E的坐标为(2,$\frac{3}{2}$),连接AE.
如图,直线AB与x轴交于点A,与y轴交于点B,与双曲线y=$\frac{k}{x}$(k>0)交于点C,过点C作CD⊥x轴于点D,过点B作BE⊥CD于点E,tan∠BCE=$\frac{3}{2}$,点E的坐标为(2,$\frac{3}{2}$),连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
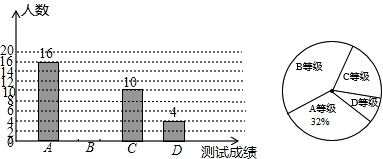
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
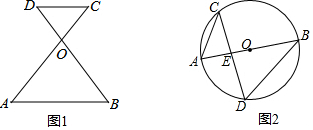
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 项目 | 物业费 | 伙食费 | 服装费 | 其他费 |
| 金额/元 | 800 | 400 |
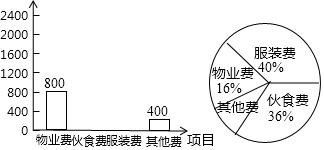
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
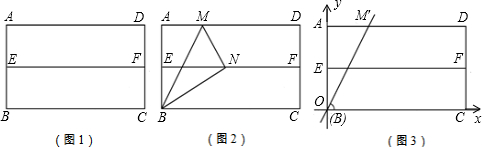
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数是104 | B. | 众数是103 | C. | 中位数是104 | D. | 方差是1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com