
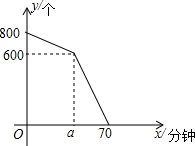
 在妇女节前后,某快递总站的快递数量不断增加,每个快递到达总站后都需要进行快递单号的扫描,妇女节当天的早上,快递总站在进行快递单号扫描前,已收到800个未扫描快递,在扫描机开始工作后,仍平均每分钟有10个未扫描快递到达快递总站,扫描机平均每分钟扫描15个快递单号.已知在扫描机开始工作a分钟内只用一台扫描机工作.在妇女节当天未扫描的快递个数y(个)与扫描机工作时间x(分钟)之间的关系如图所示.
在妇女节前后,某快递总站的快递数量不断增加,每个快递到达总站后都需要进行快递单号的扫描,妇女节当天的早上,快递总站在进行快递单号扫描前,已收到800个未扫描快递,在扫描机开始工作后,仍平均每分钟有10个未扫描快递到达快递总站,扫描机平均每分钟扫描15个快递单号.已知在扫描机开始工作a分钟内只用一台扫描机工作.在妇女节当天未扫描的快递个数y(个)与扫描机工作时间x(分钟)之间的关系如图所示.分析 (1)根据题意列出函数关系式,代入数值解答即可;
(2)利用待定系数法得出第二个解析式,再把x=55代入解答即可;
(3)设m台扫描机一起开始工作,根据题意列出方程解答即可.
解答 解:(1)设在妇女节当天扫描机工作时间x(分钟)和未扫描的快递个数y(个),
可得:y=800-(15-10)x,
把y=600代入y=800-(15-10)x,可得:x=40,
则可得a的值是40;
(2)把(40,600)和(70,0)代入y1=k1x+b1中,
可得:$\left\{\begin{array}{l}{600=40{k}_{1}+{b}_{1}}\\{0=70{k}_{1}+{b}_{1}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=-20}\\{{b}_{1}=1400}\end{array}\right.$,
所以解析式为:y1=-20x+1400;
把x=55代入y1=-20x+1400=300;
扫描机工作55分钟时,未扫描的快递个数是300个;
(3)设m台扫描机一起开始工作,可得:
30×15m=800+30×10,
解得:m=$\frac{22}{9}$,
因为m取整数,
所以m=3.
答:在妇女节当天早上只要要让3台扫描机一起开始工作.
点评 此题考查一次函数的应用,关键是根据图象得出解析式,同时利用待定系数法得出解析式.


科目:初中数学 来源: 题型:选择题
| A. | (1,1) | B. | (-1,1) | C. | (-1,-1) | D. | (1,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ②④ | D. | ④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将直线$y=\frac{{\sqrt{3}}}{3}x$向上平移2个单位交坐标轴于点A、D,然后绕AD中点B逆时针旋转60°,三条直线与y轴围成四边形ABCO,若四边形始终覆盖着二次函数y=x2-2mx+m2-1图象的一部分,则满足条件的实数m的取值范围为-$\sqrt{3}$-$\sqrt{2}$≤m≤$\sqrt{3}$.
如图,将直线$y=\frac{{\sqrt{3}}}{3}x$向上平移2个单位交坐标轴于点A、D,然后绕AD中点B逆时针旋转60°,三条直线与y轴围成四边形ABCO,若四边形始终覆盖着二次函数y=x2-2mx+m2-1图象的一部分,则满足条件的实数m的取值范围为-$\sqrt{3}$-$\sqrt{2}$≤m≤$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 每天早上小明爸爸送他上学,都会看到远处一个巨大的广告牌,小明想知道广告牌离地面有多高,于是特意测量了一下,发现A出观察广告牌底端C的仰角是20°,在B处观察广告牌底端C的仰角是53°,爸爸告诉小明刚才的车速是42千米/时,从A到B用了3秒钟,请你帮小明算一下广告牌底端离地面有多高?(温馨提示:sin53°≈$\frac{4}{5}$,cos53°≈$\frac{4}{3}$,sin20°≈$\frac{3}{10}$,cos20°≈$\frac{9}{10}$,tan20°≈$\frac{2}{5}$)
每天早上小明爸爸送他上学,都会看到远处一个巨大的广告牌,小明想知道广告牌离地面有多高,于是特意测量了一下,发现A出观察广告牌底端C的仰角是20°,在B处观察广告牌底端C的仰角是53°,爸爸告诉小明刚才的车速是42千米/时,从A到B用了3秒钟,请你帮小明算一下广告牌底端离地面有多高?(温馨提示:sin53°≈$\frac{4}{5}$,cos53°≈$\frac{4}{3}$,sin20°≈$\frac{3}{10}$,cos20°≈$\frac{9}{10}$,tan20°≈$\frac{2}{5}$)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com