
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�һ�κ���y=��2x+8��ͼ����x�ᣬy��ֱ��ڵ�A����C������A��AB��x�ᣬ����Ϊ��A������C��CB��y�ᣬ����Ϊ��C�����������ཻ�ڵ�B��
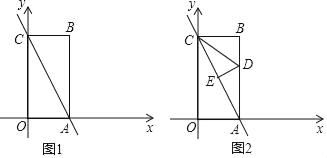
��1���߶�AB��BC��AC�ij��ֱ�ΪAB=�� ����BC=�� ����AC=�� ����
��2���۵�ͼ1�е���ABC��ʹ��A���C�غϣ��ٽ��۵����ͼ��չ�����ۺ�DE��AB�ڵ�D����AC�ڵ�E������CD����ͼ2��
�������A��B��������ѡһ��������ѡ�� ���⣮
A�������߶�AD�ij���
����y���ϣ��Ƿ���ڵ�P��ʹ�á�APDΪ���������Σ������ڣ���ֱ��д���������������е�P�����ꣻ�������ڣ���˵�����ɣ�
B�������߶�DE�ij���
��������ƽ���ڣ��Ƿ���ڵ�P������B�⣩��ʹ���Ե�A��P��CΪ��������������ABCȫ�ȣ������ڣ���ֱ��д�����з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��8��4��4![]() ����2����AD=5����P��0��2����0��8����
����2����AD=5����P��0��2����0��8����
����������������1����ȷ����OA=4��OC=8�������ó�AB=8��BC=4�����ù��ɶ������ɵó�AC��
��2��A���������۵������ʵó�BD=8��AD������ù��ɶ������ɵó�������
�ڷ�����������÷��̵�˼�뼴�ɵó�������
B���������۵������ʵó�AE�����ù��ɶ������ɵó�������
�����жϳ���APC=90�㣬�ٷ�������ۼ��㼴�ɣ�
�������1����һ�κ���y=��2x+8��ͼ����x����y��ֱ��ڵ�A����C����A��4��0����C��0��8������OA=4��OC=8��
��AB��x����CB��y������AOC=90�㣬���ı���OABC�Ǿ�������AB=OC=8��BC=OA=4����Rt��ABC�������ݹ��ɶ�������AC=![]() =4
=4![]() ��
��
�ʴ�Ϊ��8��4��4![]() ��
��
��2��A�����ɣ�1��֪��BC=4��AB=8�����۵�֪��CD=AD����Rt��BCD����BD=AB��AD=8��AD�����ݹ��ɶ�������CD2=BC2+BD2������AD2=16+��8��AD��2����AD=5�����ɢ�֪��D��4��5������P��0��y����
��A��4��0������AP2=16+y2��DP2=16+��y��5��2��
�ߡ�APDΪ�������������������������ۣ�
����AP=AD����16+y2=25����y=��3����P��0��3����0����3��
����AP=DP����16+y2=16+��y��5��2����y=![]() ����P��0��
����P��0��![]() ����
����
����AD=DP��25=16+��y��5��2����y=2��8����P��0��2����0��8����
B���١���A��֪��AD=5�����۵�֪��AE=![]() AC=2
AC=2![]() ��DE��AC��E����Rt��ADE����DE=
��DE��AC��E����Rt��ADE����DE=![]() =
=![]() ��
��
�������Ե�A��P��CΪ��������������ABCȫ�������APC�ա�ABC�����CPA�ա�ABC�����APC=��ABC=90�㣮
���ı���OABC�Ǿ��������ACO�ա�CAB����ʱ��������������P�͵�O�غ�������P��0��0������ͼ3������O��ON��AC��N����֤����AON�ס�ACO����![]() ����AN=
����AN=![]() ������N��NH��OA����NH��OA�����ANH�ס�ACO����
������N��NH��OA����NH��OA�����ANH�ס�ACO����![]() ����NH=
����NH=![]() ��AH=
��AH=![]() ����OH=
����OH=![]() ����N��
����N��![]() ��������P2���O����AC�Գ�����P2��
��������P2���O����AC�Գ�����P2��![]() ����ͬ������B����AC�ĶԳƵ�P1��ͬ�ϵķ�������P1����
����ͬ������B����AC�ĶԳƵ�P1��ͬ�ϵķ�������P1����![]() �����������������ĵ�P������Ϊ����0��0������
�����������������ĵ�P������Ϊ����0��0������![]() ��������
��������![]() ����
����


 ��ҵ����ϵ�д�
��ҵ����ϵ�д� ͬ��ѧ��һ�ζ���ϵ�д�
ͬ��ѧ��һ�ζ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ������AB��2.5�ף�����A����ǽAC�ϣ���ʱ�����¶�B��ǽ��C����Ϊ1.5�ף����ӻ�����ͣ��DE��λ���ϣ����BD��Ϊ0.5�ף������Ӷ���A�����ˣ��������ף�

A. 0.5 B. 1 C. 1.5 D. 2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������⣺��y��z��2+��x��y��2+��z��x��2=��y+z��2x��2+��z+x��2y��2+��x+y��2z��2��
��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�յ�Ǯ�����۳���Ϣ��ͼ��

��������Ϣ��С�콫�����泱���γɺ�ͷ���ҵ�֮��ľ���s��ǧ�ף���ʱ��t�����ӣ��ĺ�����ϵ��ͼ3��ʾ�����У���11��40ʱ�������泱���ij�ͷ���ҵ�12ǧ������Ϊ��A��0��12������B����Ϊ��m��0��������BC���ö��κ���s=![]() t2+bt+c��b��c�dz������̻���
t2+bt+c��b��c�dz������̻���
��1����m��ֵ���������ͷ�Ӽص��ҵص��ٶȣ�
��2��11��59ʱ��С���ﵥ�����ҵس������ؽ��߹�·��0.48ǧ��/�ֵ��ٶ����ط���ȥ���������������Ӻ��볱ͷ������
��3��������С��������ת��ͷ���ؽ��߹�·����ͷ�ٶ��볱ͷ���У�����ͷ���ҵغ���ȼ��٣�����������ٶ�Ϊ0.48ǧ��/�֣�С���������С���볱ͷ���������ͷ1.8ǧ����ʱ�䣿����ˮ���ٽ��ٶ�v=v0+![]() ��t��30����v0�Ǽ���ǰ���ٶȣ���
��t��30����v0�Ǽ���ǰ���ٶȣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ʾ����ֱ������ABCD�У���BAD=90�㣬E��ֱ��AB��һ�㣬��E��ֱ��l��BC����ֱ��CD�ڵ�F����ֱ��l����ƽ�ƣ���ƽ�ƾ���BEΪt��t��0����ֱ������ABCD��ֱ��lɨ���������ͼ����Ӱ���֣�ΪS��S����t�ĺ���ͼ����ͼ����ʾ��OMΪ�߶Σ�MNΪ�����ߵ�һ���֣�NQΪ���ߣ�N�������Ϊ4��
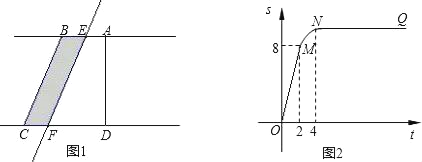
��Ϣ��ȡ
��1�������ϵij�AB=�� ����
��2��ֱ������ABCD�����=�� ����
ͼ������
��3��д��ͼ��������NQ��ʾ��ʵ�����壻
��4����2��t��4ʱ����S����t�ĺ�����ϵʽ��
������
��5����tΪ��ֵʱ��ֱ��l��ֱ������ABCD�ֳɵ����������֮��Ϊ1��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ���ĵ����ϣ������ɸ���ȫ��ͬ���ⳤΪ1cm��С������ѳ�һ�������壬��ͼ��ʾ��
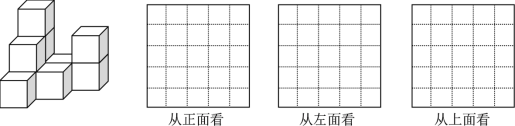
��1����������������� ����С��������ɣ��뻭�������桢���桢���濴����������������״ͼ��
��2������������ͷ����һЩ��ͬ��С�����壬������ִ�����ʹ����濴������״ͼ���䣬������������________��С�����壮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2016��Ȫ���г��������п����������ȡijУ5λͬѧһ���������Ĵ����ֱ�Ϊ��158��160��154��158��170�������������ݵõ��Ľ�������������������
A. ƽ����Ϊ160 B. ��λ��Ϊ158 C. ����Ϊ158 D. ����Ϊ20.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB��90����D��E�ֱ���AB��AC���е㣬����CD����E��EF��DC��BC���ӳ�����F��
��1��֤�����ı���CDEF��ƽ���ı��Σ�
��2�����ı���CDEF���ܳ���16cm��AC�ij�Ϊ8cm�����߶�AB�ij��ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ijУΪ�˽���꼶��ͬѧ����������������������ȡ������ͬѧ������1000���ܲ���.���ճɼ���Ϊ���㡢���á��ϸ��벻�ϸ��ĸ��ȼ�.ѧУ���������²�������ͳ��ͼ.
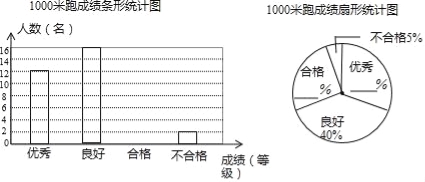
��1�����ݸ�������Ϣ����ȫ����ͳ��ͼ��
��2����У���꼶��600������������Ƴɼ�δ�ﵽ�����ж�����?
��3��ij��ס�����λ�ɼ������ͬѧ��ѡ�вμӼ������е�ѧУ�˶���1000�ױ�����Ԥ����ΪA��B��C������У�ѡ���ɳ�ǩȷ������.�ס�������ǡ�÷���ͬһ��ĸ����Ƕ���?
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com