
【题目】对于整式![]() (其中m是大于
(其中m是大于![]() 的整数).
的整数).
(1)若![]() ,且该整式是关于x的三次三项式,求m的值;
,且该整式是关于x的三次三项式,求m的值;
(2)若该整式是关于x的二次单项式,求m,n的值;
(3)若该整式是关于x的二次二项式,则m,n要满足什么条件?
【答案】(1)m=1;(2)m=-1,n=-1;(3)n=1,m为大于-2任意整数或m=-1,n≠-1或m=0,n≠4.
【解析】
(1)根据已知条件可得到关于m的方程m+2=3,解方程即可得到m的值;
(2)根据该多项式是关于x的二次单项式,可得到m+2=1,n-1=-2,据此计算即可;
(3)同样的,根据上面的分析方法,结合关于x的二次二项式的特点解答即可.
(1)因为n=2,且该多项式是关于x的三次三项式,所以原多项式变为![]() ,所以m=1,即m的值为1.
,所以m=1,即m的值为1.
(2)因为该多项式是关于x的二次单项式,
所以m+2=1,n-1=-2
解得m=-1,n=-1
(3)因为该多项式是关于x的二次二项式,
所以①![]() 这一项不存在,原多项式是关于x的二次二项式,
这一项不存在,原多项式是关于x的二次二项式,
则n-1=0,即n=1,m为大于-2任意整数
②若![]() 的次数为1,系数不为-2,原多项式是关于x的二次二项式,
的次数为1,系数不为-2,原多项式是关于x的二次二项式,
则m=-1,n≠-1
③![]() 的次数为2,系数不为3,原多项式是关于x的二次二项式,
的次数为2,系数不为3,原多项式是关于x的二次二项式,
则m=0,n≠4.


科目:初中数学 来源: 题型:
【题目】某商场服装部销售一种名牌衬衫,平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元.为了扩大销售,减少库存,商场决定降价销售,经调查,每件降价
元.为了扩大销售,减少库存,商场决定降价销售,经调查,每件降价![]() 元时,平均每天可多卖出
元时,平均每天可多卖出![]() 件.
件.
(1)若商场要求该服装部每天盈利![]() 元,每件衬衫应降价多少元?
元,每件衬衫应降价多少元?
(2)试说明每件衬衫降价多少元时,商场服装部每天盈利最多.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC中,AB=AC,点D,E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.

(1)求证:∠ABE=∠ACD;
(2)求证:过点A、F的直线垂直平分线段BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产A种产品,它的成本是6元/件,售价是8元/件,年销售量为5万件.为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x万元,产品的年销售量将是原销售量的y倍,且y与x之间满足我们学过的二种函数(即一次函数和二次函数)关系中的一种,它们的关系如下表:
x(万元) | 0 | 0.5 | 1 | 1.5 | 2 | … |
y | 1 | 1.275 | 1.5 | 1.675 | 1.8 | … |
(1)求y与x的函数关系式(不要求写出自变量的取值范围)
(2)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润W(万元)与广告费用x(万元)的函数关系式,并计算每年投入的广告费是多少万元时所获得的利润最大?
(3)如果公司希望年利润W(万元)不低于14万元,请你帮公司确定广告费的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案.已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边
表示直角三角形的两直角边![]() ,下列四个说法:①
,下列四个说法:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;其中说法正确的是
;其中说法正确的是![]()
![]()

A. ①②B. ①②③C. ①②④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
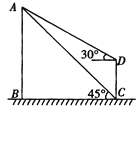
【题目】为了测量某风景区内一座塔AB的高度,某人分别在塔的对面一楼房CD的楼底C、楼顶D处,测得塔顶A的仰角为45°和30°,已知楼高CD为10m,求塔的高度。(结果精确到0.1m)(参考数据![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
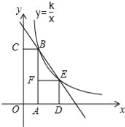
【题目】如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴,点C在y轴的正半轴上,点F再AB上,点B,E在反比例函数y=![]() 的图象上,OA=2,OC=6,则正方形ADEF的边长为______.
的图象上,OA=2,OC=6,则正方形ADEF的边长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ED为☉O的直径且ED=4,点A(不与点E,D重合)为☉O上一个动点,线段AB经过点E,且EA=EB,F为☉O上一点,∠FEB=90°,BF的延长线交AD的延长线于点C.
(1)求证:△EFB≌△ADE;
(2)当点A在☉O上移动时,直接回答四边形FCDE的最大面积为多少.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com