
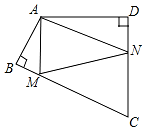
 如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N使△AMN周长最小,则∠AMN+∠ANM的度数为( )
如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N使△AMN周长最小,则∠AMN+∠ANM的度数为( )| A. | 60° | B. | 120° | C. | 90° | D. | 45° |
分析 根据要使△AMN的周长最小,即利用点的对称,让三角形的三边在同一直线上,作出A关于BC和CD的对称点A′,A″,即可得出∠AA′M+∠A″=60°,进而得出∠AMN+∠ANM=2(∠AA′M+∠A″)即可得出答案.
解答 解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.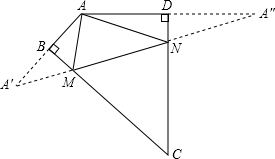
∵∠DAB=120°,
∴∠AA′M+∠A″=180°-120°=60°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×60°=120°,
故选:B.
点评 此题主要考查了平面内最短路线问题求法,以及三角形的外角的性质和垂直平分线的性质等知识的综合应用,根据轴对称的性质,得出M,N的位置是解题的关键.


科目:初中数学 来源: 题型:选择题
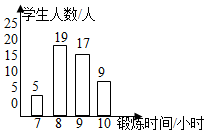 小文统计了本班同学一周的体育锻练情况,并绘制了直方图
小文统计了本班同学一周的体育锻练情况,并绘制了直方图| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8×10-6m | B. | 8×10-5m | C. | 8×10-8m | D. | 8×10-4m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-3,-7) | B. | (3,9) | C. | (3,7) | D. | (-3,-9) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.4 | B. | 0.6 | C. | 0.5 | D. | 0.65 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
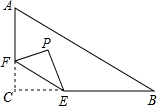 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com