
【题目】如图,在平面直角坐标系中,A(a,0),B(b,0),C(﹣1,2),且|2a﹣b+8|+(a+b﹣2)2=0.

(1)求a、b的值;
(2)如图1,点G在y轴上,三角形COG的面积是三角形ABC的面积的![]() ,求出点G的坐标;
,求出点G的坐标;
(3)如图2,过点C作CD⊥y轴交y轴于点D,点P为线段CD延长线上的一个动点,连接OP、AC、DB,OE平分∠AOP,OF⊥CE,若∠OPD+k∠DOF=k(∠FOP+∠AOE),现将四边形ABDC向下平移![]() k个单位得到四边形A1B1D1C1,已知AM+BN =
k个单位得到四边形A1B1D1C1,已知AM+BN =![]() k,求图中阴影部分的面积.
k,求图中阴影部分的面积.
【答案】(1)a=﹣2,b=4;(2)G(0,6)或(0,﹣6);(3)S阴=![]() .
.
【解析】
(1)利用非负数的性质即可解决问题;
(2)过点C作CT⊥AB于T.根据面积关系求出OG的长即可解决问题;
(3)设∠AOE=x,则∠AOP=2∠AOE=2x,∠POB=180°-2x,由CD∥AB,推出∠OPD=∠POB=180°-2x,由∠DOF=∠AOE,推出∠OPD+k∠DOF=k∠FOP+k∠AOE,推出∠OPD=k∠FOP,可得180°-2x=k(90°-x),推出k=2,即可解决问题.
(1)∵|2a﹣b+8|+(a+b﹣2)2=0,
又∵|2a﹣b+8|≥0,(a+b﹣2)2≥0,
∴![]() ,
,
解得![]() ,
,
∴a=﹣2,b=4.
(2)如图1中,过点C作CT⊥AB于T.
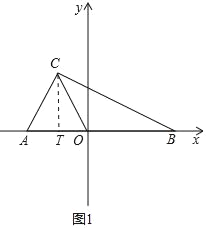
∵C(﹣1,2),
∴CT=2,
∵S△ABC=![]() ×6×2=6,
×6×2=6,
∴S△OCG=![]() ×1×OG=3,
×1×OG=3,
∴OG=6,
∴G(0,6)或(0,﹣6).
(3)如图2中,
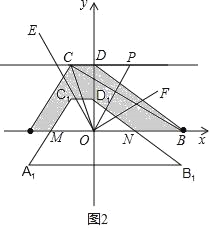
设∠AOE=x,
∵OE平分∠AOP,
∴∠AOP=2∠AOE=2x,
∵∠AOB=180°,
∴∠POB=180°﹣2x,
∵CD⊥y轴,AB⊥y轴,
∴∠CDO=∠DOB=90°,
∴CD∥AB,
∴∠OPD=∠POB=180°﹣2x,
∵OF⊥OE,
∴∠FOP=90°﹣x,
∵∠AOD=90°,
∴∠AOE+∠EOD=∠DOF+∠EOD=90°,
∴∠DOF=∠AOE,
∴∠OPD+k∠DOF=k∠FOP+k∠AOE,
∴∠OPD=k∠FOP,
∴180°﹣2x=k(90°﹣x),
∴k=2,
∴![]() ,
,
∴AM+BN=![]() ,
,
∴S阴=S四边形MNB1A1=![]() .
.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力。如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点 C为一海港,且点 C与直线 AB上两点A,B的距离分别为300km和400km,又 AB=500km,以台风中心为圆心周围250km以内为受影响区域。

(1)海港C受台风影响吗?为什么?
(2)若台风的速度为20km/h,台风影响该海港持续的时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
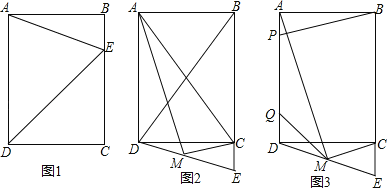
【题目】已知:如图,在矩形ABCD中,AB=6,BC=8,E为直线BC上一点.
(1)如图1,当E在线段BC上,且DE=AD时,求BE的长;
(2)如图2,点E为BC延长长线上一点,若BD=BE,连接DE,M为ED的中点,连接AM,CM,求证:AM⊥CM;
(3)如图3,在(2)条件下,P,Q为AD边上的两个动点,且PQ=5,连接PB、MQ、BM,求四边形PBMQ的周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴交于点A,与y轴交于点B,与直线y2=x交于点E,点E的横坐标为3.
与x轴交于点A,与y轴交于点B,与直线y2=x交于点E,点E的横坐标为3.
(1)直接写出b的值:b=______;
(2)当x取何值时,0<y1≤y2?
(3)在x轴上有一点P(m,0),过点P作x轴的垂线,与直线![]() 交于点C,与直线y2=x交于点D,若CD=2OB,求m的值.
交于点C,与直线y2=x交于点D,若CD=2OB,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作发现:
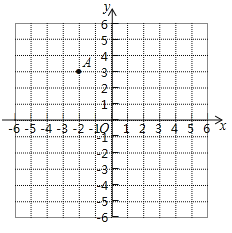
(1)如图,在平面直角坐标系中有一点![]() ,将点
,将点![]() 先向右平移3个单位长度,再向下平移3个单位长度得到点
先向右平移3个单位长度,再向下平移3个单位长度得到点![]() ,则点
,则点![]() 的坐标为 ;并在图中画出直线
的坐标为 ;并在图中画出直线![]() 的函数图象;
的函数图象;
(2)直接写出直线![]() 的解析式 ;
的解析式 ;
(3)若直线![]() 上有一动点
上有一动点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
①直接写出点![]() 的坐标 ;
的坐标 ;
②若点![]() 位于第四象限,直接写出三角形
位于第四象限,直接写出三角形![]() 的面积 .(用含
的面积 .(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
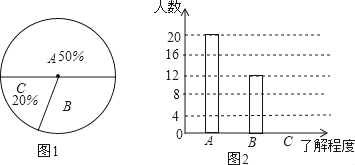
【题目】为传播奥运知识,小刚就本班学生对奥运知识的了解程度进行了一次调查统计:A:熟悉,B:了解较多,C:一般了解.图1和图2是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)在条形图中,将表示“一般了解”的部分补充完整;
(2)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数为______;
(3)如果全年级共1000名同学,请你估算全年级对奥运知识“了解较多”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列命题:①两条直线被第三条直线所截,同位角相等;②0.1的算术平方根是0.01;③算术平方根等于它本身的数是1;④如果点P(3-2n,1)到两坐标轴的距离相等,则n=1;⑤若a2=b2,则a=b;⑥若![]() =
=![]() ,则a=b.其中假命题的个数是( )
,则a=b.其中假命题的个数是( )
A. 3个B. 4个C. 5个D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com