练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．如图，把一个长方形纸片沿EF折叠后，点D，C分别落在点D′，C′的位置，若∠EFB=70°，则∠AED′等于（　　）
    A．40°B．50°C．65°D．70°

    分析 由平行可求得∠DEF，又由折叠的性质可得∠DEF=∠D′EF，结合平角可求得∠AED′．

    解答 解：∵四边形ABCD为矩形，
    ∴AD∥BC，
    ∴∠DEF=∠EFB=70°，
    又由折叠的性质可得∠D′EF=∠DEF=70°，
    ∴∠AED′=180°-70°-70°=40°，
    故选A．

    点评 本题主要考查平行线的性质及折叠的性质，掌握两直线平行内错角相等是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    5．某校随机抽查了10名参加2017年我市初中学业水平考试学生的体育成绩，得到的结果如表：
    成绩/分5657585960
    人数12124
    下列说法中，正确的是（　　）
    A．这10名学生体育成绩的中位数为58B．这10名学生体育成绩的平均数为58
    C．这10名学生体育成绩的众数为60D．这10名学生体育成绩的方差为60

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

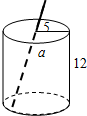    6．如图是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，已知一条到达底部的直吸管在罐内部分的长度为a，若直吸管在罐外部分还剩余3，则吸管的总长度b（罐壁的厚度和小圆孔的大小忽略不计）范围是（　　）
    A．12≤b≤13B．12≤b≤15C．13≤b≤16D．15≤b≤16

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．M（1，a）是一次函数y=3x+2与反比例函数y=$\frac{k}{x}$图象的公共点，将一次函数y=3x+2的图象向下平移4个单位得到的解析式为y=k?x+b
    （1）求y=k?x+b和y=$\frac{k}{x}$的解析式；
    （2）若A1（x1，x2），A2（x2，y2），A3（x3，y3）为双曲线y=$\frac{k}{x}$上三点，且x1＜0＜x2＜x3，请直接写出y1，y2，y3大小关系；
    （3）画出图象，观察图象直接写出不等式k?x+b＞$\frac{k}{x}$的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，线段AB=10cm，C是线段AB上一点，AC=4cm，M是AB的中点，N是AC的中点．
    求（1）线段CM的长；（2）求线段MN的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．解不等式组$\left\{\begin{array}{l}{6x+15＞2（4x+3）}\\{\frac{2x-1}{3}≥\frac{1}{2}x-\frac{2}{3}}\end{array}\right.$，并求其整数解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．解下列方程
    （1）10x+7=12x-5
    （2）1-$\frac{4-3x}{4}$=$\frac{5x+3}{6}-x$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．接下列方程：
    （1）3-（4x-3）=7；
    （2）1-$\frac{x+11}{3}$=2x+$\frac{2-x}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，反比例函数y=$\frac{k}{x}$与一次函数y=ax+b的图象交于点A（2，2），B（$\frac{1}{2}$，n）．
    （1）求这两个函数解析式；
    （2）根据图象直接回答：在第一象限内，当x满足条件$\frac{1}{2}$＜x＜2时，一次函数大于反比例函数的值；
    （3）将一次函数y=ax+b的图象沿y轴向下平移m个单位，使平移后的图象与反比例函数y=$\frac{k}{x}$的图象有且只有一个交点，求m的值．

    查看答案和解析>>

    同步练习册答案