
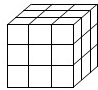
 将一个正方体木块涂成红色,然后如图把它的棱三等分,再沿等分线把正方体切开,可以得到27个小正方体.观察并回答下列问题:
将一个正方体木块涂成红色,然后如图把它的棱三等分,再沿等分线把正方体切开,可以得到27个小正方体.观察并回答下列问题:分析 (1)三面涂色的为8个角上的正方体,两面涂色的为八条棱上除去三面涂色的正方体的个数,没有涂色的用正方体总数减去三面、两面及一面涂色的正方体;
(2)根据已知图形中没有涂色的小正方形个数得出变化规律进而得出答案;
(3)由(2)得将这个正方体的棱n等分,有(n-2)3个是各个面都没有涂色的,列方程即可得到结论.
解答 (1)如图②,把正方体的棱三等分,然后沿等分线把正方体切开,得到27个小正方体.观察其中三面被涂色的有8个,两面涂色的有12个; 各面都没有涂色的有1个,故答案为:8,12,1;
(2)根据正方体的棱三等分时三面被涂色的有8个,有1个是各个面都没有涂色的,
正方体的棱四等分时三面被涂色的有8个,有8个是各个面都没有涂色的,
∴正方体的棱n等分时三面被涂色的有8个,有(n-2)3个是各个面都没有涂色的,
故答案为:8,(n-2)3;
(3)由(2)得将这个正方体的棱n等分,有(n-2)3个是各个面都没有涂色的,
∴(n-2)3=100,∵43<100<53,
∴4<n-2<5,
∴6<n<7,∴至少应该将此正方体的棱7等分,
故答案为:7.
点评 主要考查了图形的变化类问题及立体图形的认识和用特殊归纳一般规律的方法.关键是通过正方体的特点来得到有关涂色情况的规律.


科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD中,P是BC边上一点(不与点B,C重合),AP⊥PE.
如图,在正方形ABCD中,P是BC边上一点(不与点B,C重合),AP⊥PE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x<2-$\sqrt{2}$ | B. | x<2$\sqrt{2}$-1 | C. | x<2 | D. | x<$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,AB,AC是⊙O的切线,B,C是切点,过$\widehat{BC}$上的任意一点P作⊙O的切线与AB,AC分别交于点D,E.
已知:如图,AB,AC是⊙O的切线,B,C是切点,过$\widehat{BC}$上的任意一点P作⊙O的切线与AB,AC分别交于点D,E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | abcm2 | B. | (ab+2)cm2 | C. | a•b•$\frac{1}{2}$cm2 | D. | $\frac{1}{2}$abcm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com