
【题目】如图,直线y=kx+2与x轴、y轴分别交于点A、B,点C(1,a)是该直线与双曲线y=![]() 的一个交点,过点C作CD垂直y轴,垂足为D,且S△BCD=1.
的一个交点,过点C作CD垂直y轴,垂足为D,且S△BCD=1.
(1)求双曲线的解析式.
(2)设直线与双曲线的另一个交点为E,求点E的坐标.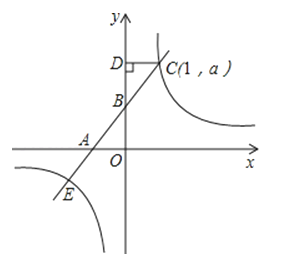
【答案】解:(1)∵△BCD的面积为1,
∴![]() 即BD=2,
即BD=2,
又∵点B是直线y=kx+2与y轴的交点,
∴点B的坐标为(0,2).
∴点D的坐标为(0,4),
∵CD⊥y轴;
∴点C的纵坐标为4,即a=4,
∵点C在双曲线上,
∴将x=1,y=4,代入y=![]() ,得m=4,
,得m=4,
∴双曲线的解析式为y=![]() ;
;
(2)∵点C(1,4)在直线y=kx+2上,
∴4=k+2,k=2,
∴直线AB的解析式为y=2x+2.
联立方程组: ,解得
,解得![]()
![]() 经检验,是方程组的解,
经检验,是方程组的解,
故E(﹣2,﹣2).
【解析】(1)先根据△BCD的面积是1求出BD的值,进而得出B、D两点的坐标求出a的值,再把点C的坐标代入双曲线y=![]() 的即可求出双曲线的解析式;
的即可求出双曲线的解析式;
(2)把C点坐标代入直线y=kx+2即可得出k的值,进而得出直线AB的解析式,在解直线与双曲线解析式组成的方程组即可求出点E的坐标.


科目:初中数学 来源: 题型:
【题目】若存在3个互不相同的有理数a,b,c,使得|1﹣a|+|1﹣3a|+|1﹣4a|=|1﹣b|+|1﹣3b|+|1﹣4b|=|1﹣c|+|1﹣3c|+|1﹣4c|=t,则t=
A. ![]() B.
B. ![]() C. 1 D. 2
C. 1 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于关于x的一元二次方程x2﹣5x﹣m﹣2=0,它的一次项系数和常数项分别是( )
A.5和﹣2B.﹣5和﹣2C.5和m﹣2D.﹣5和﹣m﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小丁在研究数学问题时遇到一个定义:对于排好顺序的三个数: ![]() ,称为数列
,称为数列![]() .计算
.计算![]() ,
, ![]() ,
, ![]() 将这三个数的最小值称为数列
将这三个数的最小值称为数列![]() 的价值.例如,对于数列2,﹣1,3,因为
的价值.例如,对于数列2,﹣1,3,因为![]() ,
, ![]() ,
, ![]() ,所以数列2,﹣1,3的价值为
,所以数列2,﹣1,3的价值为![]() .
.
小丁进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的价值.如数列﹣1,2,3的价值为![]() ;数列3,﹣1,2的价值为1;….经过研究,小丁发现,对于“2,﹣1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为
;数列3,﹣1,2的价值为1;….经过研究,小丁发现,对于“2,﹣1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)数列﹣4,﹣3,2的价值为 ;
(2)将“﹣4,﹣3,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的价值的最小值为 ,取得价值最小值的数列为 (写出一个即可);
(3)将2,﹣9,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的价值的最小值为1,则a的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列有关平方根的叙述,正确的个数是( )
①如果a存在平方根,那么a>0;②如果a有两个不同的平方根,那么a>0;③如果a没有平方根,那么a<0;④如果a>0,那么a的平方根也大于0.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列判断中,正确的个数有_______个.
①斜边对应相等的两个直角三角形全等;②有两个锐角相等的两个直角三角形不一定全等;③一条直角边对应相等的两个等腰直角三角形全等;④一个锐角和一条直角边对应相等的两个直角三角形全等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com