
【题目】如图,有一张边长为6的正方形纸片ABCD,P是AD边上一点(不与点A、D重合),将正方形纸片沿EF折叠,使点B落在点P处,点C落在点G处,PG交DC于H,连接BP.
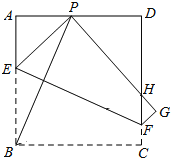
(1)求证:∠APB=∠BPH;
(2)若P为AD中点,求四边形EFGP的面积;
(3)当点P在边AD上移动时,△PDH的周长是否发生变化?写出你的结论并证明.
【答案】(1)见解析;(3)![]() ;(3)△PHD的周长不变为定值12,见解析.
;(3)△PHD的周长不变为定值12,见解析.
【解析】
(1)欲证明∠APB=∠BPH,只要证明∠APB+∠EBP=90°,∠BPH+∠EPB=90°,根据EP=EB,推出∠EBP=∠EPB即可证明.
(2)如图1中,作FM⊥AB于M.由△ABP≌△MFE,推出AP=EM=3,想办法求出EB、CF即可解决问题.
(3)△PHD的周长不变为定值12.如图2中,作BQ⊥PG于Q,连接BH,分别证明△BPA≌△BPQ和△BHQ≌△BHC即可.
(1)∵PE=BE,∴∠EBP=∠EPB.
∵∠A=∠ABC=∠EPG=90°,∴∠APB+∠EBP=90°,∠BPH+∠EPB=90°,∴∠APB=∠BPH.
(2)如图1中,作FM⊥AB于M.
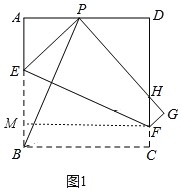
∵∠BEF+∠ABP=90°,∠BEF+∠EFM=90°,∴∠ABP=∠EFM.
在△ABP和△MFE中,∵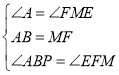 ,∴△ABP≌△MFE,∴ME=AP
,∴△ABP≌△MFE,∴ME=AP![]() AD=3.在Rt△AEP中,设AE=x,则EP=BE=6﹣x,∴(6﹣x)2=x2+32,∴x
AD=3.在Rt△AEP中,设AE=x,则EP=BE=6﹣x,∴(6﹣x)2=x2+32,∴x![]() ,∴CF=BM=AB﹣AE﹣EM
,∴CF=BM=AB﹣AE﹣EM![]() ,∴S四边形EFGP
,∴S四边形EFGP![]() (CF+BE)×BC
(CF+BE)×BC![]() (
(![]() )×6
)×6![]() .
.
(3)△PHD的周长不变为定值12.证明如下:
如图2中,作BQ⊥PG于Q,连接BH.
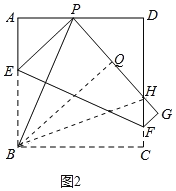
由(1)可知∠APB=∠BPQ.在△BPA和△BPQ中,∵ ,∴△BPA≌△BPQ,∴AP=PQ,AB=BQ.
,∴△BPA≌△BPQ,∴AP=PQ,AB=BQ.
∵AB=BC,∴BC=BQ.
∵∠BQH=∠C=90°,BH=BH,∴△BHQ≌△BHC,∴CH=QH,∴△PDH的周长=DP+PH+DH=(DP+AP)+(CH+DH)=AD+CD=12.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于函数![]() 的四个命题:①当
的四个命题:①当![]() 时,
时, ![]() 有最小值10;②
有最小值10;②![]() 为任意实数,
为任意实数, ![]() 时的函数值大于
时的函数值大于![]() 时的函数值;③若
时的函数值;③若![]() ,且
,且![]() 是整数,当
是整数,当![]() 时,
时, ![]() 的整数值有
的整数值有![]() 个;④若函数图象过点
个;④若函数图象过点![]() 和
和![]() ,其中
,其中![]() ,
, ![]() ,则
,则![]() .其中真命题的序号是( )
.其中真命题的序号是( )
A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=30°,求∠D的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个可以自由转动的均匀转盘![]() ,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:
,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:
①分别转动转盘![]() ;
;
②两个转盘停止后,将两个指针所指份内的数字相乘(若指针停止在等份线上,那么重转一次,直到指针指向某一份为止).

【1】用列表法或树状图分别求出数字之积为3的倍数和数字之积为5的倍数的概率;
【2】小明和小亮想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小明得2分;数字之积为5的倍数时,小亮得3分.这个游戏对双方公平吗?请说明理由;认为不公平的,试修改得分规定,使游戏对双方公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在长方形纸片ABCD中,AB=mAD,其中m1,将它沿EF折叠(点E.F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD相交于点P,连接EP.设![]() ,其中0<n1.
,其中0<n1.
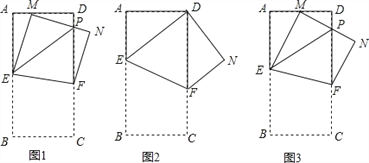
(1)如图2,当n=1(即M点与D点重合),求证:四边形BEDF为菱形;
(2)如图3,当![]() (M为AD的中点),m的值发生变化时,求证:EP=AE+DP;
(M为AD的中点),m的值发生变化时,求证:EP=AE+DP;
(3)如图1,当m=2(即AB=2AD),n的值发生变化时,![]() 的值是否发生变化?说明理由.
的值是否发生变化?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 在直线
在直线![]() 上,射线
上,射线![]() 在直线
在直线![]() 的上方,且
的上方,且![]()
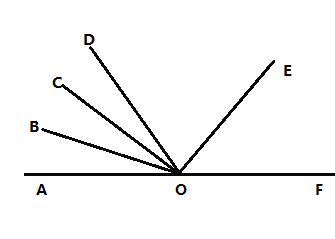
(1)如图1,![]() 在
在![]() 内部,且
内部,且![]() 平分
平分![]()
①若![]() =
=![]() ,则
,则![]() = .
= .
②若![]() =
=![]() ,则
,则![]() = .
= .
③若![]() =
=![]() ,则
,则![]() = °(用含
= °(用含![]() 的式子表示)
的式子表示)
(2)当![]() 在
在![]() 内部,且
内部,且![]() 平分
平分![]() 时,请画出图形;此时,
时,请画出图形;此时,![]() 与
与![]() 有怎样的数量关系?请说明理由.
有怎样的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
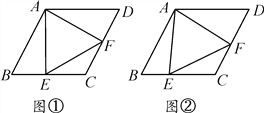
【题目】菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图①,若点E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图②,若∠EAF=60°,求证:△AEF是等边三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com