
某数学兴趣小组开展了一次活动,过程如下:
设∠BAC=θ(0°<θ<90°).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC上.
活动一:
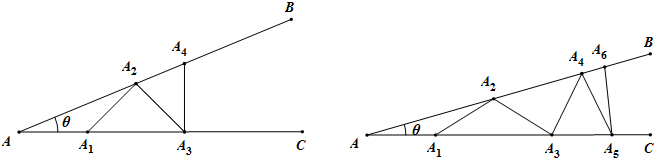
如图甲所示,从点A1开始,依次向右摆放小棒,使小棒与小棒在端点处互相垂直,A1A2为第1根小棒.
数学思考:
(1)小棒能无限摆下去吗?答: _________ .(填“能”或“不能”)
(2)设AA1=A1A2=A2A3=1.
①θ= _________ 度;
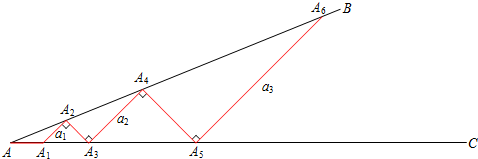
②若记小棒A2n﹣1A2n的长度为an(n为正整数,如A1A2=a1,A3A4=a2,…)求出此时a2,a3的值,并直接写出an(用含n的式子表示).

活动二:
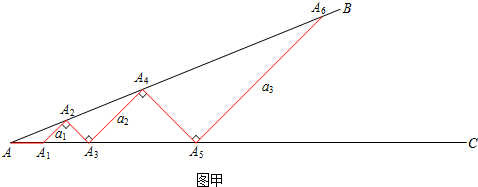
如图乙所示,从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第1根小棒,且A1A2=AA1.
数学思考:
(3)若已经摆放了3根小棒,θ1= _________ ,θ2= _________ ,θ3= _________ ;(用含θ的式子表示)
(4)若只能摆放4根小棒,求θ的范围.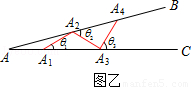
(1)能 (2)①θ=22.5° ② (3)θ1=2θ,θ2=3θ,θ3=4θ
(3)θ1=2θ,θ2=3θ,θ3=4θ
(4)18°≤θ<22.5°
【解析】
试题分析:(1)能.
因为角的两条边为两条射线,没有长度,所以小棒可以无限摆放下去;
(2)①∵AA1=A1A2=A2A3=1,A1A2⊥A2A3
∴θ2=45°,
θ=22.5°.
故答案为22.5;
②∵AA1=A1A2=A2A3=1,A1A2⊥A2A3,
∴A1A3=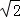 ,AA3=
,AA3=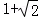 .
.
又∵A2A3⊥A3A4,
∴A1A2∥A3A4.
同理:A3A4∥A5A6,
∴∠A=∠AA2A1=∠AA4A3=∠AA6A5,
∴AA3=A3A4,AA5=A5A6
∴a2=A3A4=AA3=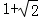 ,
,
a3=AA3+A3A5=a2+A3A5.
∵A3A5=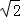 a2,
a2,
∴a3=A5A6=AA5= .
.
∴ ;
;
(3)∵A1A2=AA1
∴θ1=∠A2A1A3=2θ,
∴θ2=∠A2A4A3=θ+2θ=3θ,
∴θ3=∠A2A4A3+θ=4θ,
故答案为θ1=2θ,θ2=3θ,θ3=4θ;
(4)由题意得:
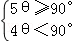 ,
,
∴18°≤θ<22.5°.
考点:相似三角形的判定与性质;一元一次不等式组的应用;勾股定理;等腰直角三角形.
点评:本题主要考查相似三角形的判定和性质、勾股定理、解一元一次不等式、等腰直角三角形的性质等知识点,解题的关键在于找到等量关系,求相关角的度数等.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| 13 |
| 9 |
| 13 |
| 16 |
| 13 |
| 13 |
| 4 |
| 6 |
| 13 |
| 4 |
| 6 |
| 41 |
| m |
| m |
| m |
| b |
| 2a |
| b |
| 2a |
| 37 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com