
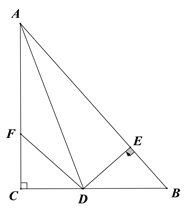
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF.
(1)求证:CF=EB.
(2)若AF=2,EB=1,求AB的长.

【答案】(1)证明见解析;(2)4
【解析】(1)由AD为角平分线,利用角平分线定理得到DE=DC,再由BD=DF,利用HL得到三角形FCD与三角形BDF全等,利用全等三角形对应边相等即可得证;
(2)利用AAS得到三角形ACD与三角形AED全等,利用全等三角形对应边相等得到AC=AE,由AB=AE+EB,等量代换即可得证.
(1)证明:∵ AD是∠BAC的平分线,∠C=90°,DE⊥AB
∴ DC=DE
∵ BD=DF
∴Rt△DCF≌Rt△DEB
∴CF=EB
(2)解:由(1)知CF=EB=1
∴AC=AF+FC=3
又∵Rt△ACD≌Rt△AED(HL或AAS)
∴AC=AE=3
∴AB=AE+EB=3+1=4
“点睛“此题考查了全等三角形的判定与性质,以及角平分线性质,熟练掌握全等三角形的判定与性质是解本题的关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】某农机厂4月份生产零件50万个,第二季度共生产零件182万个.设该厂5,6月份平均每月的增长率为x,那么x满足的方程是( )
A. 50(1+x)2=182; B. 50+50(1+x)+50(1+x)2=182
C. 50(1+2x)=182; D. 50+50(1+x)+50(1+2x)=182
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列计算中,不能用平方差公式计算的是( )
A. (m-n)(-m+n) B. (x3-y3)(x3+y3)
C. (-a-b)(a-b) D. (c2–d2)(d2+c2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)某工厂为了扩大生产,决定购买6台机器用于生产零件,现有甲、乙两种机器可供选择.其中甲型机器每日生产零件106个,乙型机器每日生产零件60个,经调査,购买3台甲型机器和2台乙型机器共需要31万元,购买一台甲型机器比购买一台乙型机器多2万元
(1)求甲、乙两种机器每台各多少万元?
(2)如果工厂期买机器的预算资金不超过34万元,那么你认为该工厂有哪几种购买方案?
(3)在(2)的条件下,如果要求该工厂购进的6台机器的日产量能力不能低于380个,那么为了节约资金.应该选择哪种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在20人的青年歌手比赛中,规定前10 名晋级,某个选手想知道自己能否晋级,应该选取( ).
A. 平均数 B. 众数 C. 中位数 D. 方差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com