

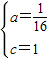
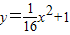 ;
;

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
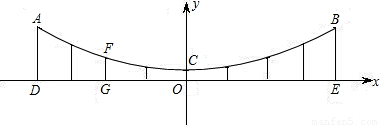
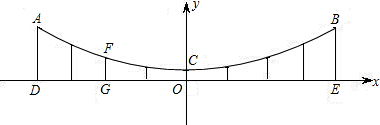
(10分)桂林红桥位于桃花江上,是桂林两江四湖的一道亮丽的风景线,该桥的部分横截面如图所示,上方可看作是一个经过A、C、B三点的抛物线,以桥面的水平线为X轴,经过抛物线的顶点C与X轴垂直的直线为Y轴,建立直角坐标系,已知此桥垂直于桥面的相邻两柱之间距离为2米(图中用线段AD、CO、BE等表示桥柱)CO=1米,FG=2米
(1) 求经过A、B、C三点的抛物线的解析式。
(2) 求柱子AD的高度。
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(20):2.6 何时获得最大利润(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com