

���� ��1��ֱ���жϡ�DCB�ա�DCM���ɵó����ۣ�
��2���ɶԳƵó�BD=AD����ϣ�1���Ľ��۵ó�AD=DM������������ʽ���ɵó����ۣ�
��3�����á�BCQ�ס�BHO���ó�$\frac{BC}{BH}=\frac{BQ}{BO}$�٣����ý�ƽ���߶����ó�$\frac{BC}{AC}=\frac{BQ}{AQ}$�ڣ�����ƽ���߷��߶γɱ����������ɵó�$\frac{CG}{AC}=\frac{OQ}{AQ}$�ܣ�����������������ʽ���ɵó����ۣ�
��� �⣺��1����ͼ1��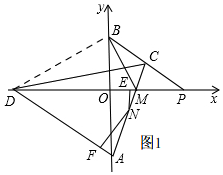 ����BD��
����BD��
��CDƽ�֡�ACB��x���ڵ�D��
���DCB=��DCM��
�ڡ�DCB�͡�DCM�У�$\left\{\begin{array}{l}{CB=CM}\\{��DCB=��DCM}\\{CD=CD}\end{array}\right.$��
���DCB�ա�DCM��
��BD=MD��
��2��NE+NF��ֵ�Dz������仯��
���ɣ���ͼ2��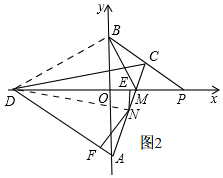 ����BD��DN��
����BD��DN��
��A��B��0��2���������x��Գƣ�
��BD=AD��
�ɣ�1��֪��BD=MD��
��AD=MD��
��NE��PD��E��NF��AD��F��
��S��ADM=S��DMN+S��DAN=$\frac{1}{2}$DM•NE+$\frac{1}{2}$AD•NF=$\frac{1}{2}$DM•NE+$\frac{1}{2}$DM•NF=$\frac{1}{2}$DM•��NE+NF����
��OA��DM��
��S��ADM=$\frac{1}{2}$DM•OA��
��$\frac{1}{2}$DM•��NE+NF��=$\frac{1}{2}$DM•OA��
��NE+NF=OA��
��B��0��2����
��OB=2��
��A��B��0��2���������x��Գƣ�
��OA=OB=2��
��NE+NF=2��
����NE+NF�Ƕ�ֵ��Ϊ2��
��3��$\frac{AC-BH}{CG}$��ֵ�Dz������仯��
���ɣ���ͼ3��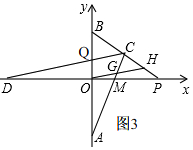 ����A��B��0��2���������x��Գƣ�
����A��B��0��2���������x��Գƣ�
��OA=OB=2��
��OH��CD��
���BCQ�ס�BHO��
��$\frac{BC}{BH}=\frac{BQ}{BO}$��
��CDƽ�֡�ACB��x���ڵ�D��
��$\frac{BC}{AC}=\frac{BQ}{AQ}$�ڣ�
��ڡ¢ٵã�$\frac{BH}{AC}=\frac{BO}{AQ}$�ۣ�
��OH��CD��
��$\frac{CG}{AC}=\frac{OQ}{AQ}$�ܣ�
��ۡ¢ܵã�$\frac{BH}{CG}=\frac{BO}{OQ}$�ݣ�
��$\frac{AC-BH}{CG}$=$\frac{AC}{CG}-\frac{BH}{CG}$=$\frac{AQ}{OQ}$-$\frac{BO}{OQ}$=$\frac{AQ-BO}{OQ}$=$\frac{OA+OQ-BO}{OQ}$=1��
����$\frac{AC-BH}{CG}$��ֵ�Ƕ�ֵ��Ϊ1��
���� �����Ǽ��α任�ۺ��⣬��Ҫ������ȫ�������ε��ж������ʣ���Գƣ�ƽ���߷��߶γɱ������������������ε��ж������ʣ���ƽ���ߵ����ʶ������Ȿ��Ĺؼ��ǵó�����ʽ�����������Ĵ����ó������ǽⱾ����ѵ㣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
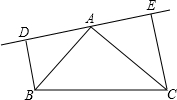 ��ͼ���ڡ�ABC�У�AB=AC��DE�ǹ���A��ֱ�ߣ�BD��DE��D��CE��DE�ڵ�E����B��C��DE��ͬ�ࣨ��ͼ��ʾ����AD=CE����֤��AB��AC��
��ͼ���ڡ�ABC�У�AB=AC��DE�ǹ���A��ֱ�ߣ�BD��DE��D��CE��DE�ڵ�E����B��C��DE��ͬ�ࣨ��ͼ��ʾ����AD=CE����֤��AB��AC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
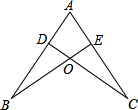 ��֪����D��AB�ϣ���E��AC�ϣ�BE��CD�ཻ�ڵ�O��AD=AE����B=��C�� ��֤��CD=BE��
��֪����D��AB�ϣ���E��AC�ϣ�BE��CD�ཻ�ڵ�O��AD=AE����B=��C�� ��֤��CD=BE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
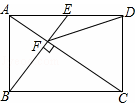 ��ͼ���ھ���ABCD�У�E��AD�ߵ��е㣬BE��AC�ڵ�F������DF����������������ۣ��١�AEF�ס�CAB����CF=2AF����DF=DC����tan��CAD=$\sqrt{2}$����S�ı���CDEF=$\frac{5}{2}$S��ABF��������ȷ�Ľ����Т٢ڢۢݣ�
��ͼ���ھ���ABCD�У�E��AD�ߵ��е㣬BE��AC�ڵ�F������DF����������������ۣ��١�AEF�ס�CAB����CF=2AF����DF=DC����tan��CAD=$\sqrt{2}$����S�ı���CDEF=$\frac{5}{2}$S��ABF��������ȷ�Ľ����Т٢ڢۢݣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
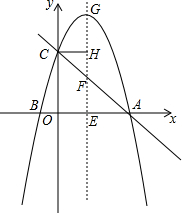 ��֪������y=ax2+bx+4��x�ύ��A��B���㣬��y�ύ�ڵ�C����B������Ϊ��-1��0������x����һ��E��EG��x�ύ�������ڵ�G����ֱ��AC�ڵ�F��
��֪������y=ax2+bx+4��x�ύ��A��B���㣬��y�ύ�ڵ�C����B������Ϊ��-1��0������x����һ��E��EG��x�ύ�������ڵ�G����ֱ��AC�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
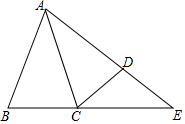 ��ͼ��ABC�У�AB=AC=8����BAC=30�㣬�ֽ���ABC�Ƶ�A��ʱ����ת30��õ���ACD���ӳ�AD��BC���ڵ�E����DE�ij���4$\sqrt{3}$-4��
��ͼ��ABC�У�AB=AC=8����BAC=30�㣬�ֽ���ABC�Ƶ�A��ʱ����ת30��õ���ACD���ӳ�AD��BC���ڵ�E����DE�ij���4$\sqrt{3}$-4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
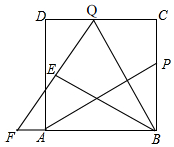 ��ͼ��PΪ�߳�Ϊ6��������ABCD�ı�BC��һ���㣨P��B��C���غϣ���Q��CD�ϣ���CQ=BP������AP��BQ������BQC��BQ���ڵ�ֱ�߷��۵õ���BQE���ӳ�QE��BA���ӳ����ڵ�F��
��ͼ��PΪ�߳�Ϊ6��������ABCD�ı�BC��һ���㣨P��B��C���غϣ���Q��CD�ϣ���CQ=BP������AP��BQ������BQC��BQ���ڵ�ֱ�߷��۵õ���BQE���ӳ�QE��BA���ӳ����ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ƽ��ֱ������ϵxOy�У�������y=-x2+mx+n��x�ύ�ڵ�A��B��A��B����ࣩ��
��ƽ��ֱ������ϵxOy�У�������y=-x2+mx+n��x�ύ�ڵ�A��B��A��B����ࣩ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com