
| 队员1 | 队员2 | 队员3 | 队员4 | 队员5 | 队员6 | |
| 甲组 | 176 | 177 | 175 | 176 | 177 | 175 |
| 乙组 | 178 | 175 | 170 | 174 | 183 | 176 |
| A. | $\overline{x}$甲=$\overline{x}$乙,S甲2<S乙2 | B. | $\overline{x}$甲=$\overline{x}$乙,S甲2>S乙2 | ||
| C. | $\overline{x}$甲<$\overline{x}$乙,S甲2<S乙2 | D. | $\overline{x}$甲>$\overline{x}$乙,S甲2>S乙2 |
分析 先根据平均数的定义分别计算出甲乙的平均数,然后根据方程公式计算出甲乙的方差即可对各选项进行判断.
解答 解:$\overline{{x}_{甲}}$=$\frac{1}{6}$(176+177+175+176+177+175)=176(cm),
$\overline{{x}_{乙}}$=$\frac{1}{6}$(178+175+170+174+183+176)=176(cm),
S甲2=$\frac{1}{6}$[2×(176-176)2+2×(175-176)2+2×(177-176)2]=$\frac{2}{3}$,
S乙2=$\frac{1}{6}$[(178-176)2+(175-176)2+(170-176)2+(174-176)2+(183-176)2+(176-176)2]=15$\frac{2}{3}$,
所以$\overline{{x}_{甲}}=\overline{{x}_{乙}}$,S甲2<S乙2.
故选A.
点评 本题考查了方差:一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差;记住方差的计算公式可解决此题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
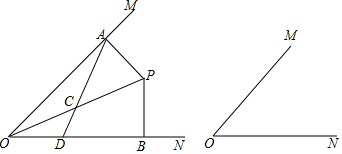
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 成绩(分) | 30 | 29 | 28 | 26 | 18 |
| 人数(人) | 32 | 4 | 2 | 1 | 1 |
| A. | 该班共有40名学生 | |
| B. | 该班学生这次考试成绩的平均数为29.4分 | |
| C. | 该班学生这次考试成绩的众数为30分 | |
| D. | 该班学生这次考试成绩的中位数为28分 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
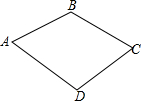 如图,在四边形ABCD中,点D在线段AB、BC的垂直平分线上,若∠D=110°,则∠B度数为( )
如图,在四边形ABCD中,点D在线段AB、BC的垂直平分线上,若∠D=110°,则∠B度数为( )| A. | 110° | B. | 115° | C. | 120° | D. | 125° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
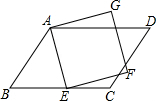 如图,?ABCD中,E为BC边上一点,以AE为边作正方形AEFG,若∠BAE=40°,∠CEF=15°,则∠D的度数是( )
如图,?ABCD中,E为BC边上一点,以AE为边作正方形AEFG,若∠BAE=40°,∠CEF=15°,则∠D的度数是( )| A. | 65° | B. | 55° | C. | 70° | D. | 75° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
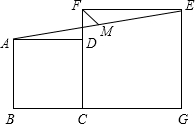 如图,正方形ABCD和正方形CGEF的边长分别是3和5,且点B、C、G在同一直线上,M是线段AE的中点,连接MF,则MF的长为$\sqrt{2}$.
如图,正方形ABCD和正方形CGEF的边长分别是3和5,且点B、C、G在同一直线上,M是线段AE的中点,连接MF,则MF的长为$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在直角坐标系中,已知点A(-3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2016的直角坐标顶点的坐标为( )
如图,在直角坐标系中,已知点A(-3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2016的直角坐标顶点的坐标为( )| A. | (8053,0) | B. | (8064,0) | C. | (8053,$\frac{12}{5}$) | D. | D、(8064,$\frac{12}{5}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
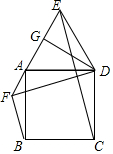 如图,正方形ABCD,过A作直线AE,过D作DG⊥AE,AG=GE,连DE.
如图,正方形ABCD,过A作直线AE,过D作DG⊥AE,AG=GE,连DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com