练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．直线AB、CD相交于O，且∠AOC+∠BOD=244°，求∠BOC的度数．

    分析 直接利用对顶角的定义得出∠AOC=∠BOD=$\frac{1}{2}$×244°，进而结合邻补角的定义得出答案．

    解答 解：∵直线AB、CD相交于点O，∠AOC+∠BOD=244°，
    ∴∠AOC=∠BOD=$\frac{1}{2}$×244°=122°，
    ∴∠BOC=58°．

    点评 此题主要考查了对顶角和邻补角，正确得出∠AOC的度数是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    13．当x取何值时，代数式x2-6x-3的值最小（　　）
    A．0B．-3C．3D．-9

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．先化简，再求值：$\frac{1}{4}$（-4a2+2a-8）-（$\frac{1}{2}$a-1），其中a=$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．计算：
    （1）16x3y3÷$\frac{1}{2}$x2y3•（-$\frac{1}{2}$xy3）；
    （2）（-ab）•（0.25a2b-$\frac{1}{2}$a3b2-$\frac{1}{6}$a4b3）÷（-0.5a2b）；
    （3）[（x2+y2）-（x-y）2+2y（x-y）]÷4y．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．若方程ax2+bx+c=0（a≠0）满足9a-3b+c=0，则方程必有一根为-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．从你学过的几何图形中举出一个轴对称图形的例子：正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．已知m，n是有理数，方程x2+mx+n=0有一个根是$\sqrt{5}$-2，则方程x2+mx+n=0的另一个根是-2-$\sqrt{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

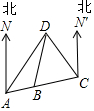    12．“奔跑吧，兄弟！”节目组，预设计一个新的游戏，“奔跑”需经A，B，C，D四点，如图，其中A，B，C三地在同一直线上，D点在A地北偏东30°方向，在C地北偏西45°方向，C地在A地北偏东75°方向．
    （1）求证：∠ACD=2∠NAD；
    （2）求∠ADC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

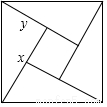    13．如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4，若用x、y表示直角三角形的两直角边（x＞y），下列四个说法：①x2+y2=49，②x•y=2，③2xy+4=49，④x+y=9．其中说法正确的是（　　）
    A．①③B．①②③C．①②④D．①②③④

    查看答案和解析>>

    同步练习册答案