
如图,已知两个菱形ABCD.CEFG,其中点A.C.F在同一直线上,连接BE、DG.
(1)在不添加辅助线时,写出其中的两对全等三角形;
(2)证明:BE=DG.
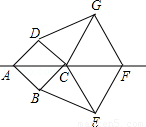
(1)△ADC≌△ABC,△GFC≌△EFC;(2)见解析
【解析】(1)解:△ADC≌△ABC,△GFC≌△EFC;
(2)证明:∵四边形ABCD.CEFG是菱形,
∴DC=BC,CG=CE,∠DCA=∠BCA,∠GCF=∠ECF,
∵∠ACF=180°,
∴∠DCG=∠BCE,
在△DCG和△BCE中
∵ ,
,
∴△DCG≌△BCE,
∴BE=DG.
(1)△ADC≌△ABC,△GFC≌△EFC,根据菱形的性质推出AD=AB,DC=BC,根据SSS即可证出结论;
(2)根据菱形性质求出DC=BC,CG=CE,推出∠DCG=∠BCE,根据SAS证出△DCG≌△BCE即可.


科目:初中数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•南昌)如图,已知两个菱形ABCD、CEFG,其中点A、C、F在同一直线上,连接BE、DG.
(2012•南昌)如图,已知两个菱形ABCD、CEFG,其中点A、C、F在同一直线上,连接BE、DG.查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(江西卷)数学(带解析) 题型:解答题
如图,已知两个菱形ABCD.CEFG,其中点A.C.F在同一直线上,连接BE、DG.
(1)在不添加辅助线时,写出其中的两对全等三角形;
(2)证明:BE=DG.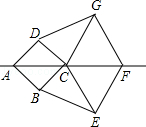
查看答案和解析>>
科目:初中数学 来源:第34章《二次函数》中考题集(35):34.4 二次函数的应用(解析版) 题型:解答题
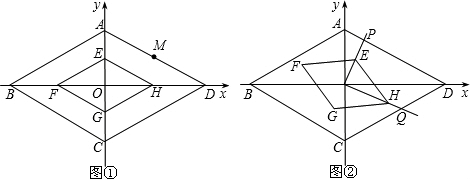
 x2经过AD的中点M.
x2经过AD的中点M.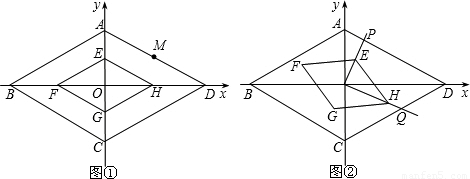
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com