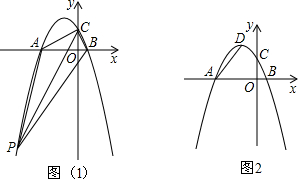
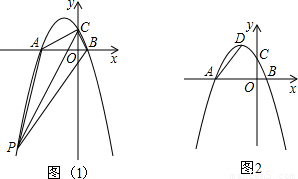
已知抛物线y=3ax2+2bx+c,
(Ⅰ)若a=b=1,c=-1,求该抛物线与x轴公共点的坐标;
(Ⅱ)若a=b=1,且当-1<x<1时,抛物线与x轴有公共点,求c的取值范围;
(Ⅲ)若a+b+c=0,且x1=0时,对应的y1>0;x2=1时,对应的y2>0,试判断当0<x<1时,抛物线与x轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
【答案】
分析:(Ⅰ)把a,b,c的值代入可得抛物线的解析式,求出两根即可;
(Ⅱ)把a,b代入解析式可得△=4-12c≥0,等于0时可直接求得c的值;求出y的相应的值后可得c的取值范围;
(Ⅲ)抛物线y=3ax
2+2bx+c与x轴公共点的个数就是一元二次方程3ax
2+2bx+c=0的实数根的个数,因此,本题的解答就是研究在不同的条件下一元二次方程3ax
2+2bx+c=0根的判别式的符号,依据判别式的符号得出相应的结论.
解答:
解:(Ⅰ)当a=b=1,c=-1时,抛物线为y=3x
2+2x-1,
方程3x
2+2x-1=0的两个根为x
1=-1,
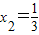
.
∴该抛物线与x轴公共点的坐标是(-1,0)和(

,0);
(Ⅱ)当a=b=1时,抛物线为y=3x
2+2x+c,且与x轴有公共点.
对于方程3x
2+2x+c=0,判别式△=4-12c≥0,有c≤

.(3分)
①当
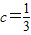
时,由方程3x
2+2x+

=0,解得x
1=x
2=-

.
此时抛物线为y=3x
2+2x+

与x轴只有一个公共点(-

,0);(4分)
②当

时,x
1=-1时,y
1=3-2+c=1+c;
x
2=1时,y
2=3+2+c=5+c.
由已知-1<x<1时,该抛物线与x轴有且只有一个公共点,考虑其对称轴为
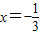
,
应有
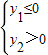
即

,
解得-5<c≤-1.
综上,

或-5<c≤-1.(6分)
(Ⅲ)对于二次函数y=3ax
2+2bx+c,
由已知x
1=0时,y
1=c>0;
x
2=1时,y
2=3a+2b+c>0,
又∵a+b+c=0,
∴3a+2b+c=(a+b+c)+2a+b=2a+b.
∴2a+b>0.
∵b=-a-c,
∴2a-a-c>0,即a-c>0.
∴a>c>0.(7分)
∵关于x的一元二次方程3ax
2+2bx+c=0的判别式△=4b
2-12ac=4(a+c)
2-12ac=4[(a-c)
2+ac]>0,
∴抛物线y=3ax
2+2bx+c与x轴有两个公共点,顶点在x轴下方.(8分)
又该抛物线的对称轴

,
由a+b+c=0,c>0,2a+b>0,
得-2a<b<-a,
∴
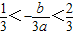
.
又由已知x
1=0时,y
1>0;
x
2=1时,y
2>0,观察图象,
可知在0<x<1范围内,该抛物线与x轴有两个公共点.(10分)
点评:借助图象,可将抽象的问题直观化;二次函数与x轴的交点的纵坐标为0;抛物线与x轴交点的个数就是一元二次方程根的个数.

 解:(Ⅰ)当a=b=1,c=-1时,抛物线为y=3x2+2x-1,
解:(Ⅰ)当a=b=1,c=-1时,抛物线为y=3x2+2x-1,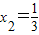 .
. ,0);
,0); .(3分)
.(3分)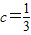 时,由方程3x2+2x+
时,由方程3x2+2x+ =0,解得x1=x2=-
=0,解得x1=x2=- .
. 与x轴只有一个公共点(-
与x轴只有一个公共点(- ,0);(4分)
,0);(4分) 时,x1=-1时,y1=3-2+c=1+c;
时,x1=-1时,y1=3-2+c=1+c;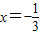 ,
,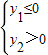 即
即 ,
, 或-5<c≤-1.(6分)
或-5<c≤-1.(6分) ,
,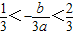 .
.

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案