
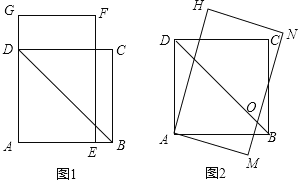
【题目】如图1,四边形ABCD是边长为![]() 的正方形,矩形AEFG中AE=4,∠AFE=30°。将矩形AEFG绕点A顺时针旋转15°得到矩形AMNH(如图2),此时BD与MN相交于点O.
的正方形,矩形AEFG中AE=4,∠AFE=30°。将矩形AEFG绕点A顺时针旋转15°得到矩形AMNH(如图2),此时BD与MN相交于点O.
(1)求∠DOM的度数;
(2)图2中,求D、N两点间的距离;
(3)若将矩形AMNH绕点A再顺时针旋转15°得到矩形APQR,此时点B在矩形APQR的内部、外部还是边上?并说明理由.
【答案】(1)120°;(2)![]() ;(3)点B在矩形APQR的内部.
;(3)点B在矩形APQR的内部.
【解析】试题分析:(1)由旋转的性质,可得∠BAM=15°,即可得∠OKB=∠AOM=75°,又由正方形的性质,可得∠ABD=45°,然后利用外角的性质,即可求得∠DOM的度数;
(2)首先连接AM,交BD于I,连接AN,由特殊角的三角函数值,求得∠HAN=30°,又由旋转的性质,即可求得∠DAN=45°,即可证得A,C,N共线,然后由股定理求得答案;
(3)在Rt△ARK中,利用三角函数即可求得AK的值,与AB比较大小,即可确定B的位置.
试题解析:(1)依题意得:∠BAM=15°,
设MN与AB交于K,
∵四边形AMNH是矩形,
∴∠M=90°,
∴∠AKM=90°-∠BAM=75°.
∴∠BKO=∠AKM=75°.
∵四边形ABCD是正方形,
∴∠ABD=45°.
∴∠DOM=∠BKO+∠ABD=75°+45°=120°.
(2)连接AN,交BD于I,连接DN
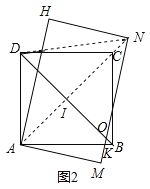
∵AE=4,∠AFE=30°,∠AEF=90°,
∴AN=AF=2AE=8.
由旋转得:∠DAH=15°,
∴∠DAN=45°.
∵正方形ABCD中,∠DAC=45°.
∴A、C、N共线.
∵正方形ABCD中,BD⊥AC,AD=AB=![]() ,
,
∴DI=AI=![]() .
.
∴NI=AN-AI=8-3=5.
∴Rt△DIN中, ![]() .
.
(3)点B在矩形APQR的内部,理由如下:
如图,
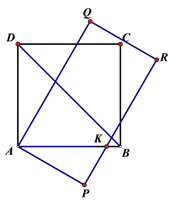
依题意得:∠BAP=15°+15°=30°,
∵∠P=90°,
∴AK=2PK.
∵AP=4,AP2+PK2=AK2,
解得: ![]() ,
,
∵AB=![]() ,
,
∴点B在矩形APQR的内部.


科目:初中数学 来源: 题型:
【题目】我们约定,在平面直角坐标系![]() 中,经过象限内某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“参照线”.例如,点
中,经过象限内某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“参照线”.例如,点![]() 的参照线有:
的参照线有:![]() ,
,![]() ,
,![]() ,
,![]() (如图1).
(如图1).
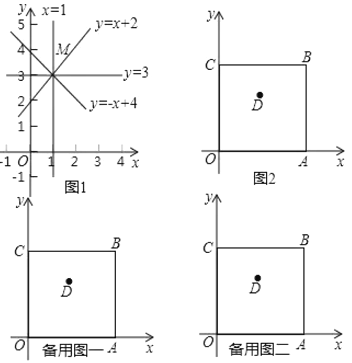
如图2,正方形![]() 在平面直角坐标系
在平面直角坐标系![]() 中,点
中,点![]() 在第一象限,点
在第一象限,点![]() ,
,![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,点
轴上,点![]() 在正方形内部.
在正方形内部.
(1)直接写出点![]() 的所有参照线: ;
的所有参照线: ;
(2)若![]() ,点
,点![]() 在线段
在线段![]() 的垂直平分线上,且点
的垂直平分线上,且点![]() 有一条参照线是
有一条参照线是![]() ,则点
,则点![]() 的坐标是_______________;
的坐标是_______________;
(3)在(2)的条件下,点![]() 是
是![]() 边上任意一点(点
边上任意一点(点![]() 不与点
不与点![]() ,
,![]() 重合),连接
重合),连接![]() ,将
,将![]() 沿着
沿着![]() 折叠,点
折叠,点![]() 的对应点记为
的对应点记为![]() .当点
.当点![]() 在点
在点![]() 的平行于坐标轴的参照线上时,写出相应的折痕
的平行于坐标轴的参照线上时,写出相应的折痕![]() 所在直线的解析式: .
所在直线的解析式: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极推进“阳光体育”工程,本学期在九年级11个班中开展篮球单循环比赛(每个班与其它班分别进行一场比赛,每班需进行10场比赛).比赛规则规定:每场比赛都要分出胜负,胜一场得3分,负一场得﹣1分.
(1)如果某班在所有的比赛中只得14分,那么该班胜负场数分别是多少?
(2)假设比赛结束后,甲班得分是乙班的3倍,甲班获胜的场数不超过5场,且甲班获胜的场数多于乙班,请你求出甲班、乙班各胜了几场.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知(a+b)2=7,(a-b)2=4,求a2+b2和ab的值.
(2)分解因式:
①x2-8xy+16y2
②(x+y+1)2-(x-y+1)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CD=CE,△ACB的顶点A在△ECD的斜边DE上,连接BD.

(1)求证:BD=AE;
(2)若AE=5cm,AD=7cm,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
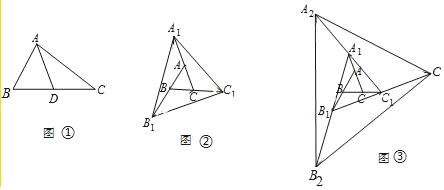
【题目】如图①,△ABC中,AD为BC边上的中线,则有S△ABD=S△ACD,许多面积问题可以转化为这个基本模型解答.如图②,已知△ABC的面积为1,把△ABC各边均顺次延长一倍,连结所得端点,得到△A1B1C1,即将△ABC向外扩展了一次,则扩展一次后的△A1B1C1的面积是_____,如图③,将△ABC向外扩展了两次得到△A2B2C2,……,若将△ABC向外扩展了n次得到△AnBnn,则扩展n次后得到的△AnBnn面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com