
【题目】如图,在△ABC中,∠C=90°,AC=BC=1,P为△ABC内一个动点,∠PAB=∠PBC,则CP的最小值为 . 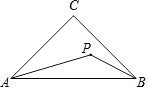
【答案】![]() ﹣1
﹣1
【解析】解:如图所示: 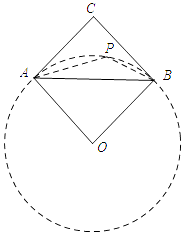
∵在△ABC中,∠C=90°,AC=BC=1,
∴∠CAB=∠CBA=45°.
又∵∠PAB=∠PBC,
∴∠PAB+∠PBA=45°.
∴∠APB=135°.
∴点P在以AB为弦的⊙O上.
∵∠APB=135°,
∴∠AOB=90°.
∴∠OAB=∠OBA=45°.
∴∠CAO=90°.
∴四边形ACBO为矩形.
∵OA=OB,
∴四边形AOBC为正方形.
∴OA=OB=1.
∴OP=1,OC= ![]() .
.
当点O、P、C在一条直线上时,PC有最小值,
∴PC的最小值=OC﹣OP= ![]() ﹣1.
﹣1.
所以答案是: ![]() ﹣1.
﹣1.
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC是弦,过点O作OE⊥BC于H交⊙O于E,在OE的延长线上取一点D,使∠ODB=∠AEC,AE与BC交于F. 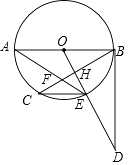
(1)判断直线BD与⊙O的位置关系,并给出证明;
(2)当⊙O的半径是5,BF=2 ![]() ,EF=
,EF= ![]() 时,求CE及BH的长.
时,求CE及BH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从背面相同的同一副扑克牌中取出红桃9张、黑桃10张、方块11张,现将这些牌洗匀背面朝上放在桌面上.
(1)求从中抽出一张牌是红桃的概率;
(2)现从桌面上先抽掉若干张黑桃,再放入与抽掉的黑桃张数相同的红桃,并洗匀且背面都朝上排开后,随机抽一张是红桃的概率不小于![]() ,问至少抽掉了多少张黑桃?
,问至少抽掉了多少张黑桃?
(3)若先从桌面上抽掉9张红桃和m(m>6)张黑桃后,再在桌面抽出一张牌.
①当m为何值时,事件“再抽出的这张牌是方块”为必然事件?
②当m为何值时,事件“再抽出的这张牌是方块”为随机事件?并求出这个事件的概率的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线![]() 与y轴交于点A.
与y轴交于点A.
(1)如图,直线![]() 与直线
与直线![]() 交于点B,与y轴交于点C,点B横坐标为
交于点B,与y轴交于点C,点B横坐标为![]() .
.
①求点B的坐标及k的值;
②直线![]() 与直线
与直线![]() 与y轴所围成的△ABC的面积等于 ;
与y轴所围成的△ABC的面积等于 ;
(2)直线![]() 与x轴交于点E(
与x轴交于点E(![]() ,0),若
,0),若![]() ,求k的取值范围.
,求k的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们来定义一种新运算:对于任意实数x、y,“※”为a※b=(a+1)(b+1)﹣1
(1)计算(﹣3)※9
(2)嘉琪研究运算“※”之后认为它满足交换律,你认为她的判断 (正确、错误)
(3)请你帮助嘉琪完成她对运算“※”是否满足结合律的证明.
证明:由已知把原式化简得a※b=(a+1)(b+1)﹣1=ab+a+b
∵(a※b)※c=(ab+a+b)※c=
a※(b※c)=
∴
∴运算“※”满足结合律.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在某市五个区投放共享单车供市民使用,投放量的分布及投放后的使用情况统计如下. 
(1)该公司在全市一共投放了万辆共享单车;
(2)在扇形统计图中,B区所对应扇形的圆心角为°;
(3)该公司在全市投放的共享单车的使用量占投放量的85%,请计算C区共享单车的使用量并补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:用2辆A型车和1辆B型车装满货物一次可运货10吨;用1辆A型车和2辆B型车装满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车![]() 辆,B型车
辆,B型车![]() 辆,一次运完,且恰好每辆车都装满货物. 根据以上信息,解答下列问题:
辆,一次运完,且恰好每辆车都装满货物. 根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC=12厘米,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为x厘米/秒,则当△BPD与△CQP全等时,x的值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,…,依此规律,第11个图案需( )根火柴.
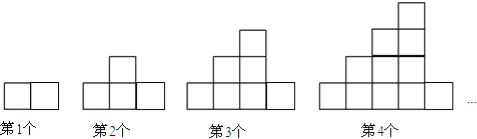
A. 156 B. 157 C. 158 D. 159
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com