
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒(0<t<![]() ),连接MN.
),连接MN.
(1)若△BMN与△ABC相似,求t的值;
(2)连接AN,CM,若AN⊥CM,求t的值.

【答案】(1)△BMN与△ABC相似时,t的值为![]() 或
或![]() ;(2)t=
;(2)t=![]()
【解析】试题分析:(1)由题意得出BM,CN, BN,BA,分两种情况讨论:①当△BMN∽△BAC时,利用相似三角形的性质得![]() ,解出t;②当△BMN∽△BCA时,
,解出t;②当△BMN∽△BCA时, ![]() ,解出t;
,解出t;
(2)过点M作MD⊥CB于点D,得到DM,BD,由BM=3tcm,CN=2tcm,得到CD,利用三角形相似的判定定理得△CAN∽△DCM,由三角形相似的性质得![]() ,解出t.
,解出t.
试题解析:(1)由题意知,BM=3tcm,CN=2tcm,∴BN=(8﹣2t)cm,BA=![]() =10(cm),当△BMN∽△BAC时,
=10(cm),当△BMN∽△BAC时, ![]() ,∴
,∴![]() ,解得:t=
,解得:t=![]() ;
;
当△BMN∽△BCA时, ![]() ,∴
,∴![]() ,解得:t=
,解得:t=![]() ,
,
∴△BMN与△ABC相似时,t的值为![]() 或
或![]() ;
;
(2)过点M作MD⊥CB于点D,由题意得:DM=BMsinB=![]() =
= ![]() (cm),BD=BMcosB=
(cm),BD=BMcosB=![]() =
= ![]() (cm),BM=3tcm,CN=2tcm,∴CD=(
(cm),BM=3tcm,CN=2tcm,∴CD=(![]() )cm,∵AN⊥CM,∠ACB=90°,∴∠CAN+∠ACM=90°,∠MCD+∠ACM=90°,∴∠CAN=∠MCD,∵MD⊥CB,∴∠MDC=∠ACB=90°,∴△CAN∽△DCM,∴
)cm,∵AN⊥CM,∠ACB=90°,∴∠CAN+∠ACM=90°,∠MCD+∠ACM=90°,∴∠CAN=∠MCD,∵MD⊥CB,∴∠MDC=∠ACB=90°,∴△CAN∽△DCM,∴![]() ,∴
,∴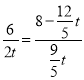 ,解得t=
,解得t=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)指出函数图象的开口方向是 ,对称轴是 ,顶点坐标为 ;
(2)当x 时,y随x的增大而减小;
(3)怎样移动抛物线![]() 就可以得到抛物线
就可以得到抛物线![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,点E为AB边上的一点,点F为对角线BD上的一点,且EF⊥AB.
(1)若四边形ABCD为正方形.
①如图①,请直接写出AE与DF的数量关系______________;
②将△EBF绕点B逆时针旋转到图②所示的位置,连接AE,DF,猜想AE与DF的数量关系并说明理由;
(2)如图③,若四边形ABCD为矩形,BC=mAB,其他条件都不变,将△EBF绕点B逆时针旋转α(0°<α<90°)得到△E′BF′,连接AE′,DF′,请在图③中画出草图,并求出AE′与DF′的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
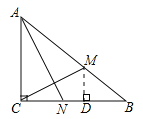
【题目】如图,已知直线y=ax+b与双曲线y=![]() (x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
(1)若A,B两点的坐标分别为(1,3),(3,y2),求点P的坐标;
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
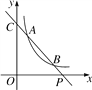
【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴上,反比例函数![]() (x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).
(x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).
(1)求反比例函数的表达式;
(2)求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=![]() (x>0)的图象经过点C,交AB于点D.已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值;
(2)连接OC,若BD=BC,求OC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
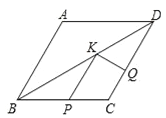
A. 1 B. ![]() C. 2 D.
C. 2 D. ![]() +1
+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com