
【题目】为了解全区5000名初中毕业生的体重情况,随机抽测了200名学生的体重,频率分布如图所示(每小组数据可含最小值,不含最大值),其中从左至右前四个小长方形的高依次为0.02、0.03、0.04、0.05,由此可估计全区初中毕业生的体重不小于60千克的学生人数约为___人.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(本小题满分10分)如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,且BF=BC.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交于点H,连接BD、FH.
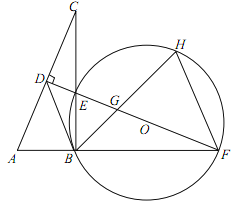
(1)求证:△ABC≌△EBF;
(2)试判断BD与⊙O的位置关系,并说明理由;
(3)若AB=1,求HGHB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
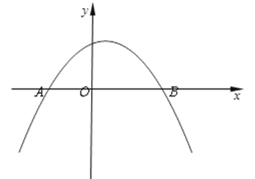
【题目】如图,已知平面直角坐标系![]() ,抛物线
,抛物线![]() 与
与![]() 轴交于点A(-2,0)和点B(4,0) .
轴交于点A(-2,0)和点B(4,0) .
(1)求这条抛物线的表达式和对称轴;
(2)点C在线段OB上,过点C作CD⊥![]() 轴,垂足为点C,交抛物线与点D,E是BD中点,联结CE并延长,与
轴,垂足为点C,交抛物线与点D,E是BD中点,联结CE并延长,与![]() 轴交于点F.
轴交于点F.
①当D恰好是抛物线的顶点时,求点F的坐标;
②联结BF,当△DBC的面积是△BCF面积的![]() 时,求点C的坐标.
时,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
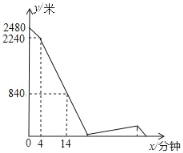
【题目】A、B两地之间的路程为2480米,甲、乙两人分别从A、B两地出发,相向而行,已知甲先出发4分钟后,乙才出发,他们两人在A、B之间的C地相遇,相遇后,甲立即返回A地,乙继续向A地前行甲到达A地时停止行走,乙到达A地时也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则乙到达A地时,甲与A地相距的路程是___米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 的坐标为
的坐标为![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 轴以每秒
轴以每秒![]() 个单位的速度向上移动,且过点
个单位的速度向上移动,且过点![]() 的直线
的直线![]() 也随之移动,如果点
也随之移动,如果点![]() 关于
关于![]() 的对称点落在坐标轴上,没点
的对称点落在坐标轴上,没点![]() 的移动时间为
的移动时间为![]() ,那么
,那么![]() 的值可以是___.
的值可以是___.
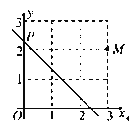
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
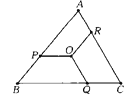
【题目】如图,点O在△ABC内,点P、Q、R分别在边AB、BC、CA上,且OP∥BC,OQ∥CA,OR∥AB,OP=OQ=OR=x,BC=a,CA=b,AB=c,则x=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com