
 ��ͼ��ʾ����֪EF��AB������ΪF��CD��AB������ΪD����1=��2�����жϡ�AGD�͡�ACB�Ƿ���ȣ�Ϊʲô�����������̲���������
��ͼ��ʾ����֪EF��AB������ΪF��CD��AB������ΪD����1=��2�����жϡ�AGD�͡�ACB�Ƿ���ȣ�Ϊʲô�����������̲������������� ��ƽ���ߵ����ʺ��ж����ó����ۣ�
��� �⣺��AGD=��ACB���������£�
��EF��AB��CD��AB����֪����
���EFB=��CDB=90�㣨 ��ֱ���� ����
��EF��CD�� ͬλ����ȣ���ֱ��ƽ�� ����
���1=��ECD�� ��ֱ��ƽ�У�ͬλ����� ��
�֡ߡ�1=��2����֪����
���ECD=��2�� �������� ����
��GD��CB�� �ڴ�����ȣ���ֱ��ƽ�� ����
���AGD=��ACB�� ��ֱ��ƽ�У�ͬλ����� ����
�ʴ�Ϊ����ֱ���壻EF��CD������ֱ��ƽ�У�ͬλ����ȣ���2���ڴ�����ȣ���ֱ��ƽ�У���ֱ��ƽ�У�ͬλ����ȣ�
���� ���⿼����ƽ���ߵ��ж������ʣ����ƽ���ߵ��ж��������ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
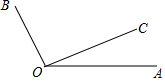 ��ͼ������OB��OC����OA��ʼ��ͬʱ�Ƶ�O��ʱ����ת��OB��ת���ٶ�Ϊÿ��6�㣬OC��ת���ٶ�Ϊÿ��2�㣮��OB��OC�غ�ʱ��OB��OCͬʱֹͣ��ת������ת��ʱ��Ϊt�룮
��ͼ������OB��OC����OA��ʼ��ͬʱ�Ƶ�O��ʱ����ת��OB��ת���ٶ�Ϊÿ��6�㣬OC��ת���ٶ�Ϊÿ��2�㣮��OB��OC�غ�ʱ��OB��OCͬʱֹͣ��ת������ת��ʱ��Ϊt�룮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ԭ���� | B�� | x���������� | C�� | y���������� | D�� | y�Ḻ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
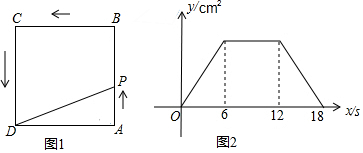
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
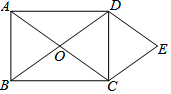 ����ABCD�Խ����ཻ��O��DE��AC��CE��BD����AD=4��CD=3�����ı���ODEC�����Ϊ6��
����ABCD�Խ����ཻ��O��DE��AC��CE��BD����AD=4��CD=3�����ı���ODEC�����Ϊ6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com