
【题目】某校在一次大课间活动中,采用了四钟活动形式:A、跑步,B、跳绳,C、做操,D、游戏.全校学生都选择了一种形式参与活动,小杰对同学们选用的活动形式进行了随机抽样调查,根据调查统计结果,绘制了不完整的统计图. 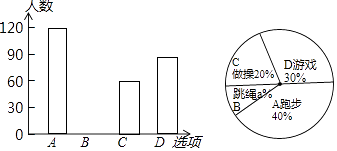
请结合统计图,回答下列问题:
(1)本次调查学生共人,a= , 并将条形图补充完整;
(2)如果该校有学生2000人,请你估计该校选择“跑步”这种活动的学生约有多少人?
(3)学校让每班在A、B、C、D四钟活动形式中,随机抽取两种开展活动,请用树状图或列表的方法,求每班抽取的两种形式恰好是“跑步”和“跳绳”的概率.
【答案】
(1)300;10;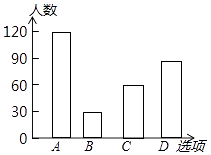
(2)解:2000×40%=800(人),
答:估计该校选择“跑步”这种活动的学生约有800人
(3)解:画树状图为:
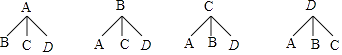
共有12种等可能的结果数,其中每班所抽到的两项方式恰好是“跑步”和“跳绳”的结果数为2,
所以每班所抽到的两项方式恰好是“跑步”和“跳绳”的概率= ![]() =
= ![]()
【解析】(1)120÷40%=300, a%=1﹣40%﹣30%﹣20%=10%,
∴a=10,
10%×300=30,
故答案为:300,10;图形如下:
(1)用A类学生数除以它所占的百分比即可得到总人数,再用1分别减去A、C、D类的百分比即可得到a的值,然后用a%乘以总人数得到B类人数,再补全条形统计图;(2)用2000乘以A类的百分比即可.(3)画树状图展示所有12种等可能的结果数,再找出每班所抽到的两项方式恰好是“跑步”和“跳绳”的结果数,然后根据概率公式求解.


 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:初中数学 来源: 题型:
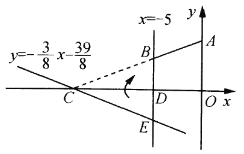
【题目】如图,在平面直角坐标系![]() 中,
中,![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴及直线
轴及直线![]() 分别交于点
分别交于点![]() .点
.点![]() 关于
关于![]() 轴对称,连接
轴对称,连接![]() .
.
(1)求点![]() 的坐标及直线
的坐标及直线![]() 的表达式;
的表达式;
(2)设面积的和![]() ,求
,求![]() 的值;
的值;
(3)在求(2)中![]() 时,嘉琪有个想法:“将
时,嘉琪有个想法:“将![]() 沿
沿![]() 轴翻折到
轴翻折到![]() 的位置,
的位置,![]() 与四边形
与四边形![]() 拼接后可看成
拼接后可看成![]() ,这样求
,这样求![]() 便转化为直接求
便转化为直接求![]() 的面积不更快捷吗?”但大家经反复验算,发现
的面积不更快捷吗?”但大家经反复验算,发现![]() ,请通过计算解释他的想法错在哪里.
,请通过计算解释他的想法错在哪里.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形 ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是
是 ![]() 的中点.过点
的中点.过点 ![]() 作
作 ![]() ,垂足为
,垂足为 ![]() .将
.将 ![]() 沿点
沿点 ![]() 到点
到点 ![]() 的方向平移,得到
的方向平移,得到 ![]() .设
.设 ![]() 、
、 ![]() 分别是
分别是 ![]() 、
、 ![]() 的中点,当点
的中点,当点 ![]() 与点
与点 ![]() 重合时,四边形
重合时,四边形 ![]() 的面积为( )
的面积为( )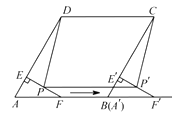
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015桂林)“全民阅读”深入人心,好读书,读好书,让人终身受益.为满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和动漫书两类图书.经了解,20本文学名著和40本动漫书共需1520元,20本文学名著比20本动漫书多440元(注:所采购的文学名著价格都一样,所采购的动漫书价格都一样).
(1)求每本文学名著和动漫书各多少元?
(2)若学校要求购买动漫书比文学名著多20本,动漫书和文学名著总数不低于72本,总费用不超过2000元,请求出所有符合条件的购书方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰![]() 中,
中,![]() =90°,
=90°,![]() 于
于![]() ,
,![]() 的平分线分别交
的平分线分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点,
两点,![]() 为
为![]() 的中点,延长
的中点,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .下列结论:①
.下列结论:① ![]() ;②
;② ![]() ;③
;③ ![]() ;④
;④![]() ;上述结论中正确的个数是( )
;上述结论中正确的个数是( )
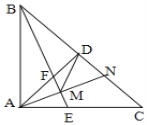
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段AB=16 cm,点C为线段AB上的一个动点(点C不与A,B重合),点D,E分别是AC和BC的中点.
(1)求DE的长;
(2)知识迁移:如图②,已知∠AOB=130°,过角的内部任一点C画射线OC,若OD,OE分别平分∠AOC和∠BOC,试说明∠DOE的大小与射线OC的位置无关.
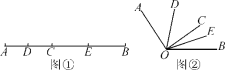
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先化简,再求值: 2(m2 mn 1) 3(![]() m2 2mn 4) ,其中 m
m2 2mn 4) ,其中 m ![]() ,n 3 .
,n 3 .
(2)已知 2a b 5 0 ,求整式 6a b 与 2a 3b 27 的和的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.
(1)直接写出∠AFC的度数: ;
(2)请你判断并写出FE与FD之间的数量关系;
(3)如图2,在△ABC中,如果∠ACB不是直角,而(1)中的其它条件不变,试判断线段AE、CD与AC之间的数量关系并说明理由.
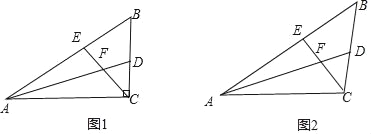
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两个分别含有30°,45°角的一副直角三角板.
(1)如图1叠放在一起
若OC恰好平分∠AOB,则∠AOD= 度;
若∠AOC=40°,则∠BOD= 度;
(2)如图2叠放在一起,∠AOD=4∠BOC,试计算∠AOC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com