
【题目】响应“家电下乡”的惠农政策,某商场决定从厂家购进甲、乙、丙三种不同型号的电冰箱80台,其中甲种电冰箱的台数是乙种电冰箱台数的2倍,购买三种电冰箱的总金额不超过132 000元.已知甲、乙、丙三种电冰箱的出厂价格分别为:1 200元/台、1 600元/台、2 000元/台
(1)至少购进乙种电冰箱多少台?
(2)若要求甲种电冰箱的台数不超过丙种电冰箱的台数,则有哪些购买方案?
【答案】(1)乙种电冰箱14台.
(2)方案一:甲种电冰箱为28台,乙种电冰箱为14台,丙种电冰箱为38台;
方案二:甲种电冰箱为30台,乙种电冰箱为15台,丙种电冰箱为35台;
方案三:甲种电冰箱为32台,乙种电冰箱为16台,丙种电冰箱为32台.
【解析】
根据购买三种电冰箱的总金额不超过132 000元,得出一元一次不等式,求出乙种冰箱的取值范围;甲种电冰箱的台数不超过丙种电冰箱的台数,得到一元一次不等式,求出乙种冰箱的取值范围.因为冰箱数为整数,得出购买方案.
(1)设购买乙种电冰箱![]() 台,则购买甲种电冰箱
台,则购买甲种电冰箱![]() 台,
台,
丙种电冰箱![]() 台,根据题意,列不等式
台,根据题意,列不等式
![]()
解这个不等式,得![]() .
.
![]() 至少购进乙种电冰箱14台.
至少购进乙种电冰箱14台.
(2)根据题意,得![]() .
.
解这个不等式,得![]() .
.
由(1)知![]() .
.
![]() .
.
又因为x为正整数,
![]() .
.
所以,有三种购买方案:
方案一:甲种电冰箱为28台,乙种电冰箱为14台,丙种电冰箱为38台;
方案二:甲种电冰箱为30台,乙种电冰箱为15台,丙种电冰箱为35台;
方案三:甲种电冰箱为32台,乙种电冰箱为16台,丙种电冰箱为32台.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某中学三班同学们就该校学生如何到校问题进行了一次调查,并将调查结果制成了条形图和扇形统计图,请你根据图表信息完成下列各题:

(1)此次共调查了___________位学生.
(2)请将条形统计图补充完整.
(3)这个学校有1000名学生,估计坐公交车的人有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
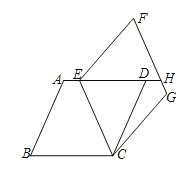
【题目】如图,完全相同的两个菱形ABCD和ECGF的顶点C重合,∠B=∠F,点E恰好在边AD上,延长ED交FG于点H.
(1)求证:∠B=∠ECB;
(2)连接BE、CH.
①试判断四边形BEHC的形状,并说理理由;
②求证:CH平分∠DCG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1.直线AD∥EF,点B,C分别在EF和AD上,∠A=∠ABC,BD平分∠CBF.
(1)求证:AB⊥BD;
(2)如图2,BG⊥AD于点G,求证:∠ACB=2∠ABG;
(3)在(2)的条件下,如图3,CH平分∠ACB交BG于点H,设∠ABG=α,请直接写出∠BHC的度数.(用含α的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种小商品的成本价为10元/kg,市场调查发现,该产品每天的销售量w(kg)与销售价x(元/kg)有如下关系w=﹣2x+100,设这种产品每天的销售利润为y(元).
(1)求y与x之间的函数关系式;
(2)当售价定为多少元时,每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某柜台销售每台进价分别为160元、120元的A.B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(进价、售价均保持不变,利润=销售收入进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,请问商场销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB=2,点P是线段AB上一点,分别以AP、BP为边作两个正方形.

(1)如果APx,求两个正方形的面积之和S;
(2)当点P是AB的中点时,求两个正方形的面积之和S1;
(3)当点P不是AB的中点时,比较(1)中的S与(2)中S1的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com