考点:待定系数法求二次函数解析式,反比例函数图象上点的坐标特征,二次函数图象上点的坐标特征,正方形的性质
专题:计算题
分析:(1)设正方形OA1P1B1边长为a,P1(a,a),代入反比例解析式求出a的值确定出P1坐标,设正方形A1A2P2B2边长为b,P2(2+b,b),同理求出b的值,确定出P2坐标;
(2)根据题意设y=a(x-2)2+2,将(0,0)代入求出a的值,即可确定出解析式;
(3)将P2横坐标代入解析式求出y的值,与纵坐标比较即可.
解答:解:(1)设正方形OA
1P
1B
1边长为a,P
1(a,a),
代入反比例解析式得:a
2=4,
解得:a
1=2,a
2=-2(舍去),即P
1(2,2),
设正方形A
1A
2P
2B
2边长为b,P
2(2+b,b),
代入反比例解析式得:b(2+b)=4,
解得:b
1=-1+
,b
2=-1-
(舍去),即P
2(1+
,-1+
);
(2)∵抛物线以P
1为顶点,
∴y=a(x-2)
2+2,
∵抛物线且经过原点,
∴0=4a+2,即a=-
,
∴y=-
x
2+2x;
(3)将x=1+
代入得:y=
-1,
∴点P
2在所求得的抛物线上.
点评:此题考查了待定系数法求二次函数解析式,反比例函数与二次函数的性质,熟练掌握待定系数法是解本题的关键.

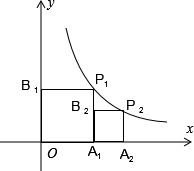 如图,正方形OA1P1B1和正方形A1A2P2B2的顶点P1,P2都在函数y=
如图,正方形OA1P1B1和正方形A1A2P2B2的顶点P1,P2都在函数y=

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案