
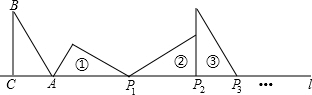
| A. | $2016+671\sqrt{3}$ | B. | $2015+672\sqrt{3}$ | C. | $2016+672\sqrt{3}$ | D. | $2015+671\sqrt{3}$ |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | x≤3且x≠-2 | B. | x≤3 | C. | x≠-2 | D. | x<3且x≠-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,AB=AC,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,下列结论:①DE=DF;②DA平分∠EDF;③AE=AF;④AD上的点到AB、AC两边距离相等.其中正确的有( )
如图,△ABC中,AB=AC,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,下列结论:①DE=DF;②DA平分∠EDF;③AE=AF;④AD上的点到AB、AC两边距离相等.其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 捐款的数额(单位:元) | 5 | 10 | 20 | 50 | 100 |
| 人数(单位:人) | 2 | 4 | 5 | 3 | 1 |
| A. | 众数是100 | B. | 中位数是30 | C. | 极差是20 | D. | 中位数是20 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 甲、乙两人进行羽毛球比赛,甲发出一个十分关键的球,出手点为P,羽毛球距地面高度h(米)与其飞行的水平距离s(米)之间的关系式为h=-$\frac{1}{12}$s2+$\frac{2}{3}$s+$\frac{3}{2}$.如图,已知球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为$\frac{9}{4}$米,设乙的起跳点C的横坐标为m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是( )
甲、乙两人进行羽毛球比赛,甲发出一个十分关键的球,出手点为P,羽毛球距地面高度h(米)与其飞行的水平距离s(米)之间的关系式为h=-$\frac{1}{12}$s2+$\frac{2}{3}$s+$\frac{3}{2}$.如图,已知球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为$\frac{9}{4}$米,设乙的起跳点C的横坐标为m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是( )| A. | 4<m<8+$\sqrt{7}$ | B. | 4-$\sqrt{7}$<m<5 | C. | 5<m<9 | D. | 5<m<4+$\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{18}$ | B. | $\frac{1}{10}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com